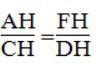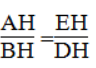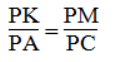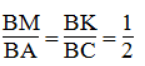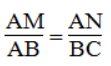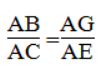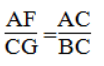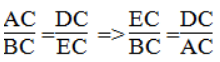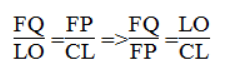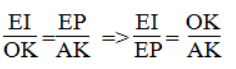Bài 55, 56, 57, 58, 59, 60 trang 98 SBT Toán 8 tập 2

---

Bài 55, 56, 57, 58, 59, 60 trang 98 SBT Toán 8 tập 2

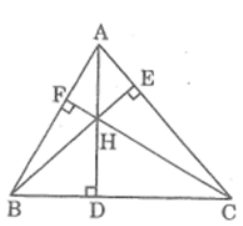
Bài 55 trang 98 sách bài tập Toán 8 Tập 2: Tam giác ABC có ba đường cao AD, BE, CF đồng quy tại H.Chứng minh rằng:AH.DH = BH.EH = CH.FH

Lời giải:

Xét ΔAFH và ΔCDH, ta có:

∠(AFH) = ∠(CDH) = 90^o

∠(AHF) = ∠(CHD) (đối đỉnh)

Suy ra: ΔAFH đồng dạng ΔCDH (g.g)

Suy ra:

Suy ra: AH.DH = CH.FH (1)

Xét ΔAEH và ΔBDH,ta có:

∠(AEH) = ∠(BDH) = 90^o

∠(AHE) = ∠(BHD) (đối đỉnh)

Suy ra: ΔAEH đồng dạng ΔBDH (g.g)

Suy ra:

Suy ra: AH.DH = BH.EH (2)

Từ (1) và (2) suy ra: AH.DH = BH.EH = CH.FH.

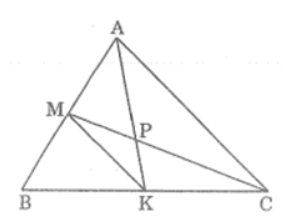
Bài 56 trang 98 sách bài tập Toán 8 Tập 2: Hai điểm M và K thứ tự nằm trên cạnh AB và BC của tam giác ABC; hai đoạn thẳng AK và CM cắt nhau tại P. Biết AP = 2PK và CP = 2PM. Chứng minh rằng AK và CM là các trung tuyến của tam giác ABC

Lời giải:

Xét ΔPAC và ΔPKM,ta có:

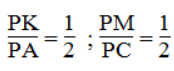
Suy ra:

Lại có:∠(APC) = ∠(KPM) (đối đỉnh)

Suy ra: ΔPKM đồng dạng ΔPAC(c.g.c) với tỉ số đồng dạng k = 1/2

Suy ra: 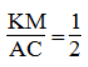(1)

Vì ΔPKM đồng dạng ΔPAC nên ∠(PKM) = ∠(PAC)

Suy ra: KM //AC (vì có cặp góc ở vị trí so le trong bằng nhau)

Trong ΔABC, ta có: KM // AC

Suy ra: ΔBMK đồng dạng ΔBAC (g.g)

Suy ra: 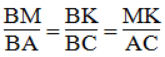(2)

Từ 1 và (2) suy ra:

Vì BM = 1/2 BA nên M là trung điểm AB.

Vì BK = 1/2 BC nên K là trung điểm BC.

Bài 57 trang 98 sách bài tập Toán 8 Tập 2: Cho hình bình hành ABCD .Từ A kẻ AM vuông góc với BC,AN vuông góc CD (M thuộc BC và N thuộc CD). Chứng mình rằng tam giác MAN đồng dạng với tam giác ABC.

Lời giải:

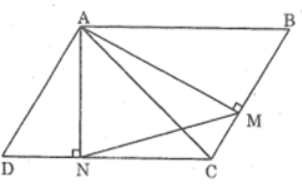
* Trường hợp góc B nhọn:

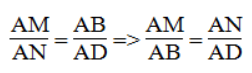
Xét ΔAMB và ΔAND, ta có:

∠(AMB) = ∠(AND) = 90^o

B = D (t/chất hình bình hành) ⇒ ΔAMB đồng dạng ΔAND (g.g)

Suy ra:

Mà AD = BC (t/chất hình hình hành)

Suy ra:

Lại có: AB // CD (gt)

AN ⊥ CD (gt)

Suy ra: AN ⊥ AB hay ∠(NAB) = 90^o

Suy ra: (NAM) + (MAB) = 90^o (1)

Trong tam giác vuông AMB ta có (ABM) = 90^o

Suy ra: ∠(MAB) + ∠B =90^o (2)

Từ (1) và (2) suy ra: (NAM) = B

Xét ΔABC và ΔMAN ta có:

(chứng minh trên)

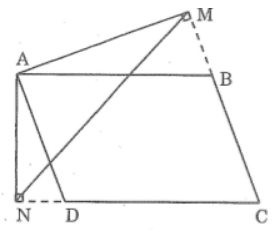
∠(NAM) = ∠B (chứng minh trên)

Vậy ΔABC đồng dạng ΔMAN (c.g.c)

* Trường hợp góc B tù:

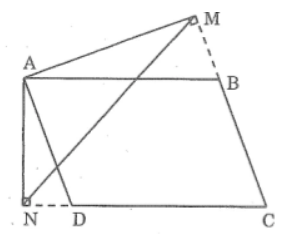
Xét ΔAMB và ΔAND, ta có:

∠(AMB) = ∠(AND) =90^o

∠(ABM) = ∠(ADN) (vì cùng bằng C)

⇒ΔAMB đông dạng ΔAND (g.g)

Suy ra:

Mà AD = BC (t/chẩt hình bình hành)

Suy ra:

Vì AB //CD nên ∠(ABC) + ∠C =180^o (3)

Tứ giác AMCN có ∠(AMC) = ∠(AND) = 90^o

Suy ra: ∠(MAN) + ∠C = 180^o (4)

Từ (3) và (4) suy ra: (MAN) = (ABC)

Xét ΔAMN và ΔABC, ta có:

(chứng minh trên)

∠(MAN) = ∠(ABC) (chứng minh trên)

Vậy ΔMAN đồng dạng ΔABC (c.g.c)

Bài 58 trang 98 sách bài tập Toán 8 Tập 2: Giả sử AC là đường chéo lớn của hình bình hành ABCD. Từ C, vẽ đường thẳng vuông góc CE với đường thẳng AB, đường vuông góc CF với đường thẳng AD (E, F thuộc phần kéo dài của các cạnh AB và AD), Chứng minh rằng AB.AE + AD.AF = AC²

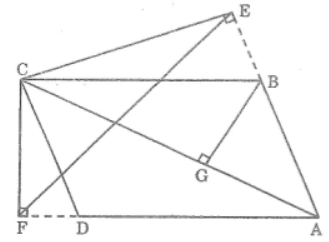
Lời giải:

Dựng BG ⊥ AC.

Xét ΔBGA và ΔCEA, ta có:

∠(BGA) = ∠(CEA) = 90^o

∠A chung

⇒ ΔBGA đồng dạng ΔCEA(g.g)

Suy ra:

AB.AE = AC.AG (1)

Xét ΔBGC và ΔCFA, ta có:

∠(BGC) = ∠(CFA) = 90^o

∠(BCG) = ∠(CAF) (so le trong vì AD //BC)

ΔBGC đồng dạng ΔCFA (g.g)

Suy ra:

⇒ BC.AF = AC.CG

Mà BC = AD (tính chất hình bình hành)

Suy ra: AD.AF = AC.CG (2)

Cộng từng vế đẳng thức (1) và (2) ta có:

AB.AE + AD.AF = AC.AG + AC.CG

AB.AE + AD.AF= AC(AG + CG)

Mà AG + CG = AC nên AB.AE + AD.AF = AC².

Bài 59 trang 98 sách bài tập Toán 8 Tập 2: Tam giác ABC có hai đường cao là AD và BE (D thuộc BC và E thuộc AC). Chứng minh hai tam giác DEC và ABC là hai tam giác đồng dạng.

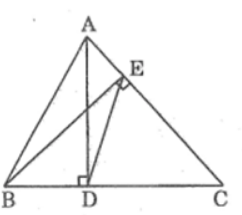
Lời giải:

Xét ΔADC và ΔBEC, ta có:

∠(ADC) =∠(BEC) = 90^o

∠C chung

Suy ra: ΔADC đồng dạng ΔBEC (g.g)

Suy ra:

⇒ EC/BC = DC/AC

Xét ΔDEC và ΔABC ta có:

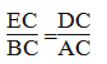
∠C chung

Vậy ΔDEC đồng dạng ΔABC (c.g.c)

Bài 60 trang 98 sách bài tập Toán 8 Tập 2: Tam giác ABC có hai đường trung tuyến AK và CL cắt nhau tại O. Từ điểm P bất kì trên cạnh AC, vẽ các đường thẳng PE song song với AK, PF song song với CL (E thuộc BC, F thuộc AB).Các trung tuyến AK, CL cắt đoạn thẳng EF theo thứ tự tại M, N. Chứng minh rằng các đoạn thẳng FM, MN, NE bằng nhau

Lời giải:

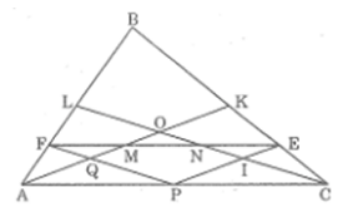
Gọi Q là giao điểm của PF và AK ,I là giao điểm của PE và CL

Trong ΔFBE ta có:PE//AK hay QM //PE

Suy ra: 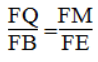(định lí ta-lét) (1)

Trong ΔALO ta có:PF //CL hay FQ //LO

Suy ra: 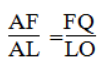(định lí ta-lét) (2)

Trong ΔALC ta có: PF // CL

Suy ra: 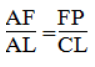(định lí ta-lét)

Từ (2) và (3) suy ra:

Vì LO = 1/3 CL (tính chất đường trung tuyến ) nên 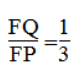(4)

Từ (1) và (4) suy ra: 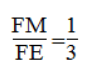⇒FM = 13 FE

Trong ΔEBF ta có:PF // CL hay NI // PE

Suy ra: 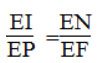(định lí ta –lét) (5)

Trong ΔCKO ta có: EI // OK

Suy ra: 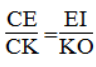(định lí ta –lét) (6)

Trong ΔCKA ta có:PE // AK

Suy ra: 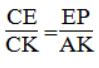(định lí ta –lét) (7)

Từ (6) và (7) suy ra:

Vì OK =1/3 AK (tính chất đường trung tuyến ) nên 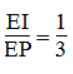(8)

Từ (5) và (8) suy ra: 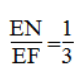⇒EN = 1/3 EF

Ta có: MN = EF - (EN + FM) = EF - (1/3 EF + 1/3 EF) = 1/3 EF

Vậy EN = MN = NF