(SGK + SBT) Giải Toán 8 trang 58 Kết nối tri thức, Chân trời sáng tạo, Cánh diều

---

Haylamdo giới thiệu lời giải bài tập Toán 8 trang 58 Kết nối tri thức, Chân trời sáng tạo, Cánh diều sẽ giúp học sinh lớp 8 dễ dàng làm bài tập Toán 8 trang 58.

(SGK + SBT) Giải Toán 8 trang 58 Kết nối tri thức, Chân trời sáng tạo, Cánh diều

- Toán lớp 8 trang 58 Tập 1 (sách mới):

• Giải Toán 8 trang 58 Chân trời sáng tạo

  Xem lời giải

• Giải Toán 8 trang 58 Cánh diều

  Xem lời giải

• Giải Toán 8 trang 58 Kết nối tri thức

  Xem lời giải

- Toán lớp 8 trang 58 Tập 2 (sách mới):

---

---

---

Lưu trữ: Giải SBT Toán 8 trang 58 (sách cũ)

Bài 54 trang 58 sách bài tập Toán 8 Tập 2: Hãy cho biết số nào trong các số 2/3 ; 2/7 ; -4/5 là nghiệm của bất phương trình 5 – 3x < (4 + 2x) – 1

Lời giải:

Ta có: 5 – 3x < (4 + 2x) – 1 ⇔ 5 – 3x < 4 + 2x – 1

⇔ -3x – 2x < 4 – 1 – 5 ⇔ -5x < -2 ⇔ x > 2/5

Vậy chỉ có giá trị 2/3 > 2/5 nên trong các số đã cho thì số 2/3 là nghiệm của bất phương trình.

Bài 55 trang 58 sách bài tập Toán 8 Tập 2: Hai quy tắc biến đổi tương đương của bất phương trình cũng giống như hai quy tắc biến đổi tương đương của phương trình. Điều đó có đúng không?

Lời giải:

Ta có, quy tắc chuyển vế của phương trình giống quy tắc chuyển vế của bất phương trình, nhưng quy tắc nhân hai vế của phương trình với cùng một số khác 0 không thể chuyển thành quy tắc nhân hai vế của bất phương trình với cùng một số khác 0, bởi vì bất phường trình sẽ đổi chiều khi ta nhân hai vế của nó với một số âm.

Bài 56 trang 58 sách bài tập Toán 8 Tập 2: Cho bất phương trình ẩn x: 2x + 1 > 2(x + 2).

a. Chứng tỏ các giá trị -5; 0; -8 đều không phải là nghiệm của nó.

b. Bất phương trình này có thể nhận giá trị nào của x là nghiệm?

Lời giải:

a. Thay giá trị của x vào từng vế của bất phương trình:

x = -5 vế trái: 2.(-5) + 1 = -10 + 1 = -9

vế phải: 2.[(-5) + 1] = 2.(-4) = -8

Vì -9 < -8 nên x = -5 không phải là nghiệm của bất phương trình.

x = 0 vế trái: 2.0 + 1 = 1

vế phải: 2.(0 + 1) = 2

Vì 1 < 2 nên x = 0 không phải là nghiệm của bất phương trình.

x = -8 vế trái: 2.(-8) + 1 = -16 + 1 = -15

vế phải: 2.[(-8) + 1] = 2.(-7) = -14

Vì -15 < -14 nên x = -8 không là nghiệm của bất phương trình.

b. Ta có: 2x + 1 > 2(x + 2)

⇔ 2x + 1 > 2x + 2

⇔ 0x > 1

Vậy bất phương trình vô nghiệm.

Bài 57 trang 58 sách bài tập Toán 8 Tập 2: Bất phương trình aane x: 5 + 5x < 5(x + 2). Có thể nhận giá trị nào của x là nghiệm?

Lời giải:

Ta có: 5 + 5x < 5(x + 2)

⇔ 5 + 5x < 5x + 10

⇔ 5x – 5x < 10 – 5

⇔ 0x < 5

Bất kì giá trị nào của x cũng thỏa mãn vế trái nhỏ hơn vế phải.

Vậy tập nghiệm của bất phương trình là tập số thực R.

Bài 58 trang 58 sách bài tập Toán 8 Tập 2: So sánh số a và số b nếu:

a. x < 5 ⇔ (a – b)x < 5(a – b)

b. x > 2 ⇔ (a – b)x < 2(a – b)

Lời giải:

a. Ta có: x < 5 ⇔ (a – b)x < 5(a – b)

⇒ a – b > 0 ⇔ a > b

b. Ta có: x > 2 ⇔ (a – b)x < 2(a – b)

⇒ a – b < 0 ⇔ a < b

Bài 59 trang 58 sách bài tập Toán 8 Tập 2: Tìm số nguyên x lớn nhất thỏa mãn mỗi bất phương trình sau:

a. 5,2 + 0,3x < - 0,5

b. 1,2 – (2,1 – 0,2x) < 4,4

Lời giải:

a. Ta có: 5,2 + 0,3x < - 0,5

⇔ 0,3x < - 0,5 – 5,2

⇔ 0,3x < - 5,7

⇔ x < -19

Vậy số nguyên lớn nhất cần tìm là -20

b. Ta có: 1,2 – (2,1 – 0,2x) < 4,4

⇔ 1,2 -2,1 + 0,2x < 4,4

⇔ 0,2x < 4,4 – 1,2 + 2,1

⇔ 0,2x < 5,3

⇔ x < 53/2

Vậy số nguyên lớn nhất thỏa mãn điều kiện là số 26.

Bài 60 trang 58 sách bài tập Toán 8 Tập 2: Tìm số nguyên x bé nhất thỏa mãn mỗi bất phương trình sau:

a. 0,2x + 3,2 > 1,5

b. 4,2 – (3 – 0,4x) > 0,1x + 0,5

Lời giải:

a. Ta có: 0,2x + 3,2 > 1,5

⇔ 0,2x > 1,5 – 3,2

⇔ 0,2x > - 1,7

⇔ x > - 17/2

Vậy số nguyên bé nhất cần tìm là – 8.

b. Ta có: 4,2 – (3 – 0,4x) > 0,1x + 0,5

⇔ 4,2 – 3 + 0,4x > 0,1x + 0,5

⇔ 0,4x – 0,1x > 0,5 – 1,2

⇔ 0,3x > - 0,7

⇔ x > - 7/3

Vậy số nguyên bé nhất cần tìm là -2.

Bài 61 trang 58 sách bài tập Toán 8 Tập 2: Với giá trị nào của m thì phương trình ẩn x:

a. x – 3 = 2m + 4 có nghiệm dương?

b. 2x – 5 = m + 8 có nghiệm số âm?

Lời giải:

a. Ta có x – 3 = 2m + 4

⇔ x = 2m + 4 + 3

⇔ x = 2m + 7

Phương trình có nghiệm số dương khi 2m + 7 > 0 ⇔ m > - 7/2

b. Ta có: 2x – 5 = m + 8

⇔ 2x = m + 8 + 5

⇔ 2x = m + 13

⇔ x = -(m + 13)/2

Phương trình có nghiệm số âm khi -(m + 13)/2 < 0 ⇔ m + 13 < 0 ⇔ m < -13

Bài 62 trang 58 sách bài tập Toán 8 Tập 2: Giải các bất phương trình:

a. (x + 2)² < 2x(x + 2) + 4

b. (x + 2)(x + 4) > (x – 2)(x + 8) + 26

Lời giải:

a. Ta có: (x + 2)² < 2x(x + 2) + 4

⇔ x² + 4x + 4 < 2x² + 4x + 4

⇔ x² + 4x – 2x² – 4x < 4 – 4

⇔ -x² < 0

⇔ x² > 0

Vậy tập nghiệm của bất phương trình là: {x|x ≠ 0}

b. Ta có: (x + 2)(x + 4) > (x – 2)(x + 8) + 26

⇔ x² + 4x + 2x + 8 > x² + 8x – 2x – 16 + 26

⇔ x² + 6x – x² < 10 – 8

⇔ 0x > 2

Vậy bất phương trình vô nghiệm.

Bài 63 trang 58 sách bài tập Toán 8 Tập 2: Giải các bất phương trình:

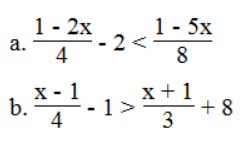
Lời giải:

⇔ 2 – 4x – 16 < 1 – 5x

⇔ -4x + 5x < 1 – 2 + 16

⇔ x < 15

Vậy tập nghiệm của bất phương trình là: {x|x < 15}

⇔ 3x – 3 – 12 > 4x + 4 + 96

⇔ 3x – 4x > 4 + 96 + 3 + 12

⇔ -x > 115 ⇔ x < -115

Vậy tập nghiệm của bất phương trình là: {x|x < -115}

Bài 64 trang 58 sách bài tập Toán 8 Tập 2: Tìm các số tự nhiên n thỏa mãn mỗi bất phương trình sau:

a. 3(5 – 4n) + (27 + 2n) > 0

b. (n + 2)² – (n – 3)(n + 3) ≤ 40

Lời giải:

a. Ta có: 3(5 – 4n) + (27 + 2n) > 0

⇔ 15 – 12n + 27 + 2n > 0

⇔ -10n + 42 > 0

⇔ -10n > -42

⇔ n < 4,2

Vậy các số tự nhiên cần tìm là 0; 1; 2; 3; 4.

b. Ta có: (n + 2)² – (n – 3)(n + 3) ≤ 40

⇔ n² + 4n + 4 – n² + 9 ≤ 40

⇔ 4n < 40 – 13

⇔ n < 27/4

Vậy các số tự nhiên cần tìm là 0; 1; 2; 3; 4; 5; 6.