(SGK + SBT) Giải Toán 8 trang 88 Kết nối tri thức, Chân trời sáng tạo, Cánh diều
Haylamdo giới thiệu lời giải bài tập Toán 8 trang 88 Kết nối tri thức, Chân trời sáng tạo, Cánh diều sẽ giúp học sinh lớp 8 dễ dàng làm bài tập Toán 8 trang 88.
(SGK + SBT) Giải Toán 8 trang 88 Kết nối tri thức, Chân trời sáng tạo, Cánh diều
- Toán lớp 8 trang 88 Tập 1 (sách mới):
- Toán lớp 8 trang 88 Tập 2 (sách mới):
Lưu trữ: Giải SBT Toán 8 trang 88 (sách cũ)
Bài 69 trang 88 SBT Toán 8 Tập 1: Vẽ hình đối xứng qua đường thẳng d của hình đã vẽ (h.6)
Lời giải:
a.
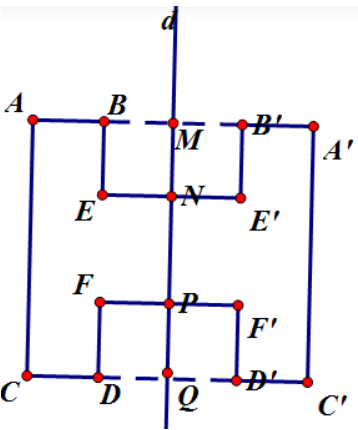
- Kéo dài AB, CD cắt d tại M, Q
- Trên tia AB lấy A', B' sao cho MB' = MB; MA' = MA
- Trên tia CD lấy C', D' sao cho QC' = QC; QD' = QD
- Trên tia EN lấy E' sao cho NE = NE'
- Trên tia FP lấy F' sao cho PF = PF'
Nối các điểm đã dựng ta được hình đối xứng qua d của hình đã cho.
b.
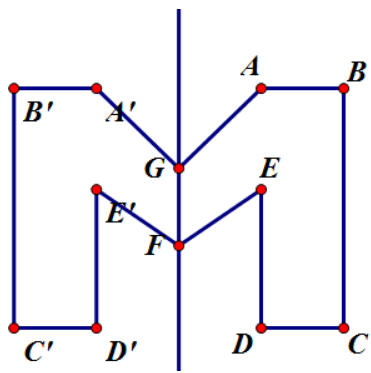
- Giả sử AB ∩ d = I; CD ∩ d = H
- Trên tia AB lấy A', B'sao cho IA = IA'; IB = IB'
- Trên tia CD lấy C', D' sao cho HC' = HC; HD' = HD
- Từ E kẻ đường vuông góc với d, cắt d tại J
- Trên EJ lấy E' sao cho JE = JE'
Nối các điểm đã dựng ta được hình đối xứng qua d của hình đã cho.
Bài 70 trang 88 SBT Toán 8 Tập 1: Điền dấu “X” vào ô thích hợp:
| Câu khẳng định | Đúng | Sai |
| a. Tam giác có một trục đối xứng là tam giác cân | ||
| b. Tứ giác có một trục đối xứng là hình thang cân |
Lời giải:
| Câu khẳng định | Đúng | Sai |
| a. Tam giác có một trục đối xứng là tam giác cân | x | |
| b. Tứ giác có một trục đối xứng là hình thang cân | x |
Bài 71 trang 88 SBT Toán 8 Tập 1: Chứng minh rằng giao điểm hai đường chéo hình thang cân nằm trên trục đối xứng của hình thang cân.
Lời giải:
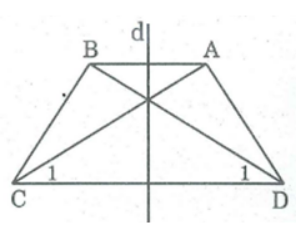
Hình thang cân ABCD có AB // CD
Gọi O là giao điểm của hai đường chéo AC và BD.
Xét ΔADC và ΔBCD:
AD = BC (tính chất hình thang cân)
AC = BD (tính chất hình thang cân)
CD chung
Do đó ΔADC= ΔBCD (c.c.c)
⇒ ∠D1 = ∠C1
⇒ ΔOCD cân tại O
⇒ OC = OD nên O nằm trên đường trung trực của CD.
Trục đối xứng hình thang cân là đường thẳng trung trực của hai đáy.
Vậy O thuộc trục đối xứng của hình thang cân.
Bài 72 trang 88 SBT Toán 8 Tập 1: Cho góc nhọn xOy, điểm A nằm trong góc đó.
Dựng điểm B thuộc tia Ox, điểm C thuộc tia Oy sao cho tam giác ABC có chu vi nhỏ nhất.
Lời giải:
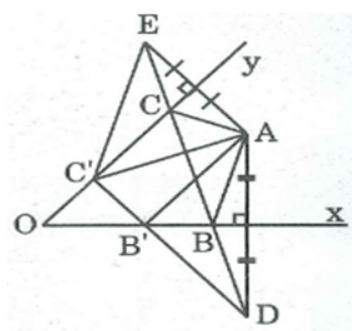
Cách dựng:
- Dựng điểm D đối xứng với A qua Ox
- Dựng điểm E đối xứng với A qua Oy
Nối DE cắt Ox tại B, Oy tại C
Tam giác ABC là tam giác có chu vi nhỏ nhất
Vì (xOy) < 90 nên DE luôn cắt Ox và Oy do đó ΔABC luôn dựng được.
Chứng minh:
Chu vi ΔABC bằng AB + BC + AC
Vì D đối xứng với A qua Ox nên OX là trung trực của AD
⇒ AB = BD (tính chất đường trung trực)
E đối xứng với A qua Oy là trung trực của AE
⇒ AC = CE (tính chất đường trung trực)
Suy ra: AB + BC + AC = BD + BC + BE = DE (1)
Lấy B' bất kì trên Ox, C' bất kì trên tia Oy. Nối C'E, C'A, B'A, B'D.
Ta có: B'A = B'D và C'A = C'E (tính chất đường trung trực)
Chu vi ΔAB'C' bằng AB'+ AO + B'C'= B'D+ B'C'+ C'E (2)
Vì DE ≤ B'D + B'C' + C'E (dấu bằng xảy ra khi B' trùng B, C' trùng C) nên chu vi của ΔABC ≤ chu vi của ΔA'B'C'
Vậy ΔABC có chu vi bé nhất.

