(SGK + SBT) Giải Toán 8 trang 62 Chân trời sáng tạo, Cánh diều

---

Haylamdo giới thiệu lời giải bài tập Toán 8 trang 62 Chân trời sáng tạo, Cánh diều sẽ giúp học sinh lớp 8 dễ dàng làm bài tập Toán 8 trang 62.

(SGK + SBT) Giải Toán 8 trang 62 Chân trời sáng tạo, Cánh diều

- Toán lớp 8 trang 62 Tập 1 (sách mới):

• Giải Toán 8 trang 62 Cánh diều

  Xem lời giải

• Giải Toán 8 trang 62 Chân trời sáng tạo

  Xem lời giải

- Toán lớp 8 trang 62 Tập 2 (sách mới):

---

---

---

Lưu trữ: Giải SBT Toán 8 trang 62 (sách cũ)

Bài 81 trang 62 sách bài tập Toán 8 Tập 2: Chứng tỏ diện tích của hình vuông có cạnh 10m không nhỏ hơn diện tích hình chữ nhật có cùng chu vi.

Lời giải:

Chu vi hình chữ nhật là 4.10 = 40 (m)

Gọi x (m) là chiều rộng hình chữ nhật. Điều kiện: x < 20.

Khi đó chiều dài hình chữ nhật là 20 – x (m).

Diện tích hình chữ nhật là x(20 – x) (m²).

Ta có: (10 – x)² ≥ 0

⇔ 102 – 20x + x² ≥ 0

⇔ 102 ≥ 20x – x²

⇔ 102 ≥ x(20 – x)

Vậy diện tích hình vuông cạnh 10m không nhỏ hơn diện tích hình chữ nhật cùng chu vi.

Bài 82 trang 62 sách bài tập Toán 8 Tập 2: Giải các bất phương trình:

a. 3(x – 2)(x + 2) < 3x² + x

b. (x + 4)(5x – 1) > 5x² + 16x + 2

Lời giải:

a. Ta có: 3(x – 2)(x + 2) < 3x² + x

⇔ 3(x² – 4) ≤ 3x² + x

⇔ 3x² – 12 ≤ 3x² + x

⇔ 3x² – 3x² – x ≤ 12

⇔ -x ≤ 12

⇔ x ≤ -12

Vậy tập nghiệm của bất phương trình là {x|x > -12}

b. Ta có: (x + 4)(5x – 1) > 5x² + 16x + 2

⇔ 5x² – x² + 20x – 4 > 5x² + 16x + 2

⇔ 5x² – x² + 20x – 5x² – 16x > 2 + 4

⇔ 3x > 6

⇔ x > 2

Vậy tập nghiệm của bất phương trình là {x|x > 2}

Bài 83 trang 62 sách bài tập Toán 8 Tập 2: Giải các bất phương trình:

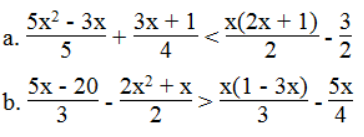
Lời giải:

a. Ta có:

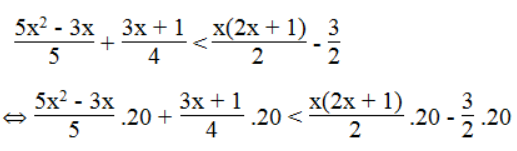
⇔ 20x² – 12x + 15x + 5 < 20x² + 10x – 30

⇔ 20x² – 12x + 15x – 20x² – 10x < -30 – 5

⇔ -7x < -35

⇔ x > 5

Vậy tập nghiệm của bất phương trình là {x|x > 5}

b. Ta có:

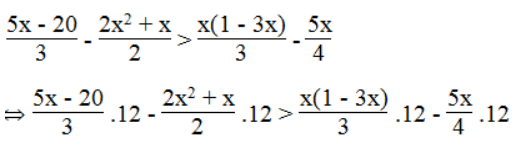
⇔ 20x – 80 – 12x² – 6x > 4x – 12x² – 15x

⇔ 20x – 12x² – 6x – 4x + 12x² + 15x > 80

⇔ 25x > 80

⇔ x > 3,2

Vậy tập nghiệm của bất phương trình là {x|x > 3,2}

Bài 84 trang 62 sách bài tập Toán 8 Tập 2: Với giá trị nào của x thì:

a. Giá trị của biểu thức 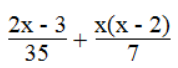không lớn hơn giá trị của biểu thức

b. Giá trị của biểu thức không nhỏ hơn giá trị của biểu thức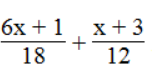

Lời giải:

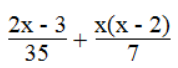
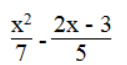
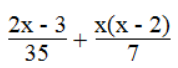
a. Giá trị của biểu thức không lớn hơn giá trị của biểu thức nghĩa là ≤

Ta có:

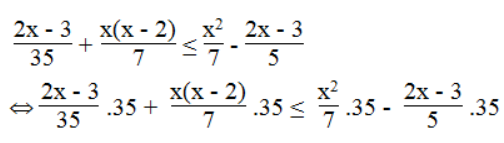
⇔ 2x – 3 + 5x² – 10x ≤ 5x² – 14x + 21

⇔ 2x + 5x² – 10x – 5x² + 14x ≤ 21 + 3

⇔ 6x ≤ 24

⇔ x ≤ 4

Vậy với x ≤ 4 thì Giá trị của biểu thức 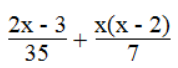không lớn hơn giá trị của biểu thức

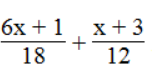
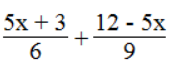
b. Giá trị của biểu thức không nhỏ hơn giá trị của biểu thức nghĩa là ≥

Ta có:

⇔ 12x + 2 + 3x + 9 ≥ 30x + 18 + 48 – 20x

⇔ 12x + 3x – 30x + 20x ≥ 18 + 48 – 2 – 9

⇔ 5x ≥ 55

⇔ x ≥ 11

Vậy với x ≥ 11 thì giá trị của biểu thức không nhỏ hơn giá trị của biểu thức

Bài 85 trang 62 sách bài tập Toán 8 Tập 2: Tìm x sao cho:

a. –x² < 0

b. (x – 1)x < 0

Lời giải:

a. Ta có: -x² < 0 ⇔ x² > 0

Mọi giá trị x ≠ 0 đều là nghiệm của bất phương trình.

Tập hợp các giá trị của x là {x ∈ R|x ≠ 0}

b. Trường hợp 1: x – 1 > và 0

Ta có: x – 1 > 0 ⇔ x > 1 và x < 0

Điều này không xảy ra: loại.

Trường hợp 2: x – 1 < 0 và x > 0

Ta có: x – 1 < 0 ⇔ x < 1 và x > 0

Suy ra: 0 < x < 1

Vậy tập hợp các giá trị của x là {x|0 < x < 1}

Bài 86 trang 62 sách bài tập Toán 8 Tập 2: Tìm x sao cho:

a. x² > 0

b. (x – 2)(x – 5) > 0

Lời giải:

a. Với x² > 0 thì mọi x khác 0 đều thỏa mãn bài toán.

Tập hợp các giá trị của x là {x ∈ R|x ≠ 0}

b. Trường hợp 1: x – 2 > 0 và x – 5 > 0

Ta có: x – 2 > 0 ⇔ x > 2

x – 5 > 0 ⇔ x > 5

Suy ra: x > 5

Trường hợp 2: x – 2 < 0 và x – 5 < 0

Ta có: x – 2 < 0 ⇔ x < 2

x – 5 < 0 ⇔ x < 5

Suy ra: x < 2

Vậy với x > 5 hoặc x < 2 thì (x – 2)(x – 5) > 0.

Bài 87 trang 62 sách bài tập Toán 8 Tập 2: Với giá trị nào của x thì:

a. (x - 2)/(x - 3) > 0

b. (x + 2)/(x - 5) < 0

Lời giải:

a. Trường hợp 1: x – 2 > 0 và x – 3 > 0

Ta có: x – 2 > 0 ⇔ x > 2

x – 3 > 0 ⇔ x > 3

Suy ra: x > 3

Trường hợp 2: x – 2 < 0 và x – 3 < 0

Ta có: x – 2 < 0 ⇔ x < 2

x – 3 < 0 ⇔ x < 3

Suy ra: x < 2

Vậy với x > 3 hoặc x < 2 thì (x - 2)/(x - 3) > 0

b. Trường hợp 1: x + 2 > 0 và x – 5 < 0

Ta có: x + 2 > 0 ⇔ x > -2

x – 5 < 0 ⇔ x < 5

Suy ra: -2 < x < 5

Trường hợp 2: x + 2 < 0 và x – 5 > 0

Ta có: x + 2 < 0 ⇔ x < -2

x – 5 > 0 ⇔ x > 5

Trường hợp trên không xảy ra.

Vậy với -2 < x < 5 thì (x + 2)/(x - 5) < 0.

Bài 88 trang 62 sách bài tập Toán 8 Tập 2: Chứng tỏ các phương trình sau vô nghiệm:

a. |2x + 3| = 2x + 2

b. |5x – 3| = 5x – 5

Lời giải:

a. Ta có: |2x + 3| = 2x + 3 khi 2x + 3 ≥ 0 ⇔ x ≥ -1,5

|2x + 3| = -2x – 3 khi 2x + 3 < 0 ⇔ x < -1,5

Ta có: 2x + 3 = 2x + 2 ⇔ 0x = -1

Phương trình vô nghiệm.

-2x – 3 = 2x + 2

⇔ -2x - 2x = 2 + 3

⇔ -4x = 5

⇔ x = -1,25

Giá trị x = -1,25 không thỏa mãn điều kiện x < -1,5 nên loại.

Vậy phương trình đã cho vô nghiệm.

b. Ta có: |5x – 3| = 5x – 3 khi 5x – 3 ≥ 0 ⇔ x ≥ 0,6

|5x – 3| = 3 – 5x khi 5x – 3 < 0 ⇔ x < 0,6

Ta có: 5x – 3 = 5x – 5 ⇔ 0x = -2

Phương trình vô nghiệm.

3 – 5x = 5x – 5

⇔ -5x – 5x = -5 – 3

⇔ -10x = -8

⇔ x = 0,8

Giá trị x = 0,8 không thỏa mãn điều kiện x < 0,6 nên loại.

Vậy phương trình đã cho vô nghiệm.