(SGK + SBT) Giải Toán 8 trang 61 Kết nối tri thức, Chân trời sáng tạo, Cánh diều

---

Haylamdo giới thiệu lời giải bài tập Toán 8 trang 61 Kết nối tri thức, Chân trời sáng tạo, Cánh diều sẽ giúp học sinh lớp 8 dễ dàng làm bài tập Toán 8 trang 61.

(SGK + SBT) Giải Toán 8 trang 61 Kết nối tri thức, Chân trời sáng tạo, Cánh diều

- Toán lớp 8 trang 61 Tập 1 (sách mới):

• Giải Toán 8 trang 61 Chân trời sáng tạo

  Xem lời giải

• Hoạt động 2 trang 61 Toán 8 Tập 1 Cánh diều

  Xem lời giải

• Giải Toán 8 trang 61 Kết nối tri thức

  Xem lời giải

- Toán lớp 8 trang 61 Tập 2 (sách mới):

---

---

---

Lưu trữ: Giải SBT Toán 8 trang 61 (sách cũ)

Bài 71 trang 61 sách bài tập Toán 8 Tập 2: Cho các bất đẳng thức:

a > b; a < b; c > 0; c < 0; a + c < b + c; a + c > b + c; ac < bc; ac > bc

Hãy điển các bất đẳng thức thích hợp vào chỗ trống (...) trong câu sau: Nếu……… và………. thì………..

Lời giải:

Nếu a > b và c > 0 thì ac > bc

Nếu a > b và c > 0 thì a + c > b + a

Nếu a > b và c < 0 thì a + c > b + c

Nếu a > b và c < 0 thì ac < bc

Nểu a < b và c > 0 thì ac < bc

Nếu a < b và c > 0 thì a + c < b + c

Nếu a < b và c < 0 thì ac > bc

Nếu a < b và c < 0 thì a + c < b + c

Bài 72 trang 61 sách bài tập Toán 8 Tập 2: Cho a > b, chứng tỏ:

a. 3a + 5 > 3b + 2

b. 2 – 4a < 3 – 4b

Lời giải:

a. Ta có: a > b ⇔ 3a > 3b ⇔ 3a + 5 > 3b + 5 (1)

Mặt khác: 3b + 5 > 3b + 2 (2)

Từ (1) và (2) suy ra: 3a + 5 > 3b + 2

b. Ta có: a > b ⇔ -4a < -4b ⇔ 3 – 4a < 3 – 4b (1)

Mặt khác: 2 – 4a < 3 – 4a (2)

Từ (1) và (2) suy ra: 2 – 4a < 3 – 4b

Bài 73 trang 61 sách bài tập Toán 8 Tập 2: a. Chứng tỏ 2,99 là nghiệm của bất phương trình 3 > x. Hãy kể ra bốn số lớn hơn 2,99 là nghiệm của bất phương trình đó.

b. Chứng tỏ 4,01 là nghiệm của bất phương trình 4 < x. Hãy kể ra ba số nhỏ hơn 4,01 là nghiệm của bất phương trình đó.

Lời giải:

a. Ta có 2,99 là nghiệm của bất phương trình x < 3. Bốn số lớn hơn 2,99 là nghiệm của bất phương trình là: 2,999; 2,998; 2,997; 2,996.

b. Ta có 4,01 là nghiệm của bất phương trình x > 4. Ba số nhỏ hơn 4,01 là nghiệm của bất phương trình là: 4,003; 4,002; 4,001.

Bài 74 trang 61 sách bài tập Toán 8 Tập 2: Giải các bất phương trình và biểu diễn tập nghiệm của chúng trên trục số.

a. 2(3x – 1) – 2x < 2x + 1

b. 4x – 8 ≥ 3(3x – 2) + 4 – 2x

Lời giải:

a. Ta có: 2(3x – 1) – 2x < 2x + 1

⇔ 6x – 2 – 2x < 2x – 1

⇔ 6x – 2x – 2x < -1 + 2

⇔ 2x < 1

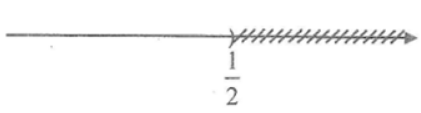
⇔ x < 12

Vậy tập nghiệm của bất phương trình là {x|x < 12 }

b. Ta có: 4x – 8 ≥ 3(3x – 2) + 4 – 2x

⇔ 4x – 8 ≥ 9x – 6 + 4 – 2x

⇔ 4x – 9x + 2x ≥ - 6 + 4 + 8

⇔ -3x ≥ 6

⇔ x ≤ -2

Vậy tập nghiệm của bất phương trình là {x|x ≤ -2}

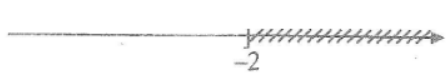
Bài 75 trang 61 sách bài tập Toán 8 Tập 2: Giải các bất phương trình:

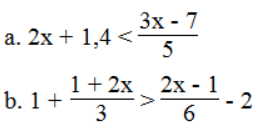
Lời giải:

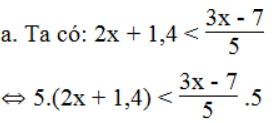
⇔ 10x + 7 < 3x – 7

⇔ 10x – 3x < -7 – 7

⇔ 7x < -14

⇔ x < -2

Vậy tập nghiệm của bất phương trình là {x|x < -2}

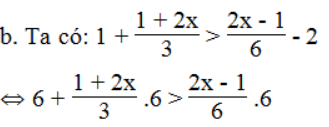
⇔ 6 + 2 + 4x > 2x – 1 – 12

⇔ 4x – 2x > -1 – 12 – 6 – 2

⇔ 2x > -21

⇔ x > -10,5

Vậy tập nghiệm của bất phương trình là {x|x > -10,5}

Bài 76 trang 61 sách bài tập Toán 8 Tập 2: Một người đi bộ quảng đường dài 18km trong khoảng thời gian không nhiều hơn 4 gỉờ. Lúc đầu người đó đi với vận tốc 5km/h, về sau đi với vận tốc 4km/h. Xác định độ dài đoạn đường mà người đó đã đi với vận tốc 5km/h.

Lời giải:

Gọi x (km) là đoạn đường người đó đi với vận tốc 5km/h. ĐK: x < 18.

Khi đó đoạn đường người đó đi với vận tốc 4km/h là 18 – x(km)

Thời gian đi với vận tốc 5km/h là x/5 giờ

Thời gian đi với vận tốc 4km/h là (18 - x)/4 giờ.

Vì thời gian đi hết đoạn đường không quá 4 giờ nên ta có bất phương trình: x/5 + (18 - x)/4 ≤ 4.

Ta có: x/5 + (18 - x)/4 ≤ 4

⇔ x/5 .20 + (18 - x)/4 .20 ≤ 4.20

⇔ 4x + 90 – 5x ≤ 80

⇔ 4x – 5x ≤ 80 – 90

⇔ -x ≤ -10

⇔ x ≥ 10

Vậy đoạn đường đi với vận tốc 5km/h ít nhất là 10km.

Bài 77 trang 61 sách bài tập Toán 8 Tập 2: Giải các phương trình:

a. |2x| = 3x – 2

b. |-3,5x| = 1,5x + 5

c. |x + 15| = 3x – 1

d. |2 – x| = 0,5x – 4

Lời giải:

a. Ta có: |2x| = 2x khi 2x ≥ 0 ⇒ x ≥ 0

|2x| = -2x khi 2x < 0 ⇒ x < 0

Ta có: 2x = 3x – 2

⇔ 2x – 3x = -2

⇔ x = 2

Giá trị x = 2 thỏa mãn điều kiện x ≥ 0 nên 2 là nghiệm của phương trình.

-2x = 3x – 2

⇔ -2x – 3x = -2

⇔ x = 25

Giá trị x = 25 không thỏa mãn điều kiện x < 0 nên loại.

Vậy tập nghiệm của phương trình là S = {2}

b. Ta có: |-3,5x| = -3,5x khi -3,5x ≥ 0 ⇒ x ≤ 0

|-3,5x| = 3,5x khi -3,5x < 0 ⇒ x > 0

Ta có: -3,5x = 1,5x + 5

⇔ -3,5x – 1,5x = 5

⇔ -5x = 5

⇔ x = -1

Giá trị x = -1 thỏa mãn điều kiện x ≤ 0 nên -1 là nghiệm của phương trình.

3,5x = 1,5x + 5

⇔ 3,5x – 1,5x = 5

⇔ 2x = 5

⇔ x = 2,5

Giá trị x = 2,5 thỏa mãn điều kiện x > 0 nên 2,5 là nghiệm của phương trình.

Vậy tập nghiệm của phương trình là S = {-1; 2,5}

c. Ta có: |x + 15| = x + 15 khi x + 15 ≥ 0 ⇒ x ≥ -15

|x + 15| = -x – 15 khi x + 15 < 0 ⇒ x < -15

Ta có: x + 15 = 3x – 1

⇔ x – 3x = -1 – 15

⇔ -2x = -16

⇔ x = 8

Giá trị x = 8 thỏa mãn điều kiện x ≥ -15 nên 8 là nghiệm của phương trình.

-x – 15 = 3x – 1

⇔ -x – 3x = -1 + 15

⇔ -4x = 14

⇔ x = -3,5

Giá trị x = -3,5 không thỏa mãn điều kiện x < -15 nên loại.

Vậy tập nghiệm của phương trình là S = {8}

d. Ta có: |2 – x| = 2 – x khi 2 – x ≥ 0 ⇒ x ≤ 2

|2 – x| = x – 2 khi 2 – x < 0 ⇒ x > 2

Ta có: 2 – x = 0,5x – 4

⇔ -x – 0,5x = -4 + 2

⇔ 0,5x = -2

⇔ x = -4

Giá trị x = -4 thỏa mãn điều kiện x ≤ 2 nên loại.

x – 2 = 0,5x – 4

⇔ x – 0,5x = -4 + 2

⇔ 0,5x = -2

⇔ x = -4

Giá trị x = -4 không thỏa mãn điều kiện x > 2 nên loại.

Vậy tập nghiệm của phương trình là S = ∅.

Bài 78 trang 61 sách bài tập Toán 8 Tập 2: Chứng tỏ rằng, trong một tam giác độ dài một cạnh luôn nhỏ hơn nửa chu vi.

Lời giải:

Gọi a, b, c lần lượt là độ dài ba cạnh của tam giác.

Chu vi tam giác là a + b + c.

Theo bất đẳng thức tam giác, ta có:

a < b + c

⇔ a + a < a + b + c

⇔ 2a < a + b + c

⇔ a < (a + b + c)/2

Tương tự:

b < a + c

⇔ b + b < a + b + c

⇔ 2b < a + b + c

⇔ b < (a + b + c)/2

c < a + b

⇔ c + c < a + b + c

⇔ 2c < a + b + c

⇔ c < (a + b + c)/2

Vậy trong một tam giác độ dài một cạnh luôn nhỏ hơn nửa chu vi.

Bài 79 trang 61 sách bài tập Toán 8 Tập 2: Với số m và số n bất kì, chứng tỏ rằng:

a. (m + 1)² ≥ 4m

b. m² + n² + 2 ≥ 2(m + n)

Lời giải:

a. Ta có: (m – 1)² ≥ 0

⇔ (m – 1)² + 4m ≥ 4

⇔ m² – 2m + 1 + 4m ≥ 4m

⇔ m² + 2m + 1 ≥ 4m

⇔ (m + 1)² ≥ 4m

b. Ta có: (m – 1)² ≥ 0; (n – 1)² ≥ 4m

⇒ (m – 1)² + (n – 1)² ≥ 0

⇔ m² – 2m + 1 + n² – 2n + 1 ≥ 0

⇔ m² + n² + 2 ≥ 2(m + n)

Bài 80 trang 61 sách bài tập Toán 8 Tập 2: Cho a ≥ 0 và b ≥ 0, chứng tỏ rằng: (a + b)(1a + 1b ) ≥ 4

Lời giải:

Ta có: (a – b)² ≥ 0

⇔ a² + b² – 2ab ≥ 0

⇔ a² + b² – 2ab + 2ab ≥ 2ab

⇔ a² + b² ≥ 2ab

Vì a ≥ 0, b ≥ 0 nên ab ≥ 0 ⇒ 1/ab ≥ 0

(a² + b²).1/ab ≥ 2ab.1/ab

⇔ a/b + b/a ≥ 2

⇔ 2 + a/b + b/a ≥ 2 + 2

⇔ 2 + a/b + b/a ≥ 4

⇔ 1 + 1 + a/b + b/a ≥ 4

⇔ a/b + b/a + a/b + b/a ≥ 4

⇔ a(1/a + 1/b ) + b(1/a + 1/b ) ≥ 4

⇔ (a + b)(1/a + 1/b ) ≥ 4