(SGK + SBT) Giải Toán 8 trang 90 Kết nối tri thức

---

Haylamdo giới thiệu lời giải bài tập Toán 8 trang 90 Kết nối tri thức sẽ giúp học sinh lớp 8 dễ dàng làm bài tập Toán 8 trang 90.

(SGK + SBT) Giải Toán 8 trang 90 Kết nối tri thức

- Toán lớp 8 trang 90 Tập 1 (sách mới):

• HĐ1 trang 90 Toán 8 Tập 1 Kết nối tri thức

  Xem lời giải

- Toán lớp 8 trang 90 Tập 2 (sách mới):

---

---

---

Lưu trữ: Giải SBT Toán 8 trang 90 (sách cũ)

Bài 81 trang 90 SBT Toán 8 Tập 1: Chu vi hình bình hành ABCD bằng l0cm, chu vi tam giác ABD bằng 9cm. Tính độ dài BD.

Lời giải:

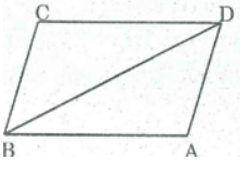
Chu vì hình bình hành ABCD bằng 10cm nên (AB + AD).2 = 10(cm)

⇒ AB + AD = 10 : 2 = 5(cm)

Chu vi của ΔABD bằng:

AB + AD + BD = 9(cm)

⇒ BD = 9 - (AB + AD) = 9 - 5 = 4(cm)

Bài 82 trang 90 SBT Toán 8 Tập 1: Hình bên dưới, cho ABCD là hình bình hành. Chứng minh rằng AE //CF.

Lời giải:

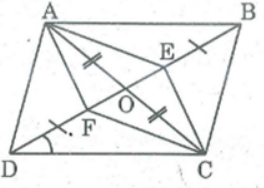
Gọi O là giao điểm của AC và BD, ta có:

OA = OC (tính chất hình bình hành)

OB = OD

Xét ΔAEB và ΔCFD, ta có:

AB = CD (tính chất hình bình hành)

∠(ABE) = ∠(CDF) (so le trong)

BE = DF (gt)

Do đó: ΔAEB = ΔCFD (c.g.c) ⇒ BE = DF

Ta có: OB = OE + BE

OD = OF + BF

Suy ra: OE = OF

Suy ra tứ giác AECF là hình bình hành (vì có 2 đường chéo cắt nhau tại trung điểm của mỗi đường) ⇒ AE // CF.

Bài 83 trang 90 SBT Toán 8 Tập 1: Cho hình hình hành ABCD. Gọi E, F theo thứ tự là trung điểm của AB, CD. Gọi M là giao điểm của AF và DE, N là giao điểm của BF và CE. Chứng minh rằng:

a. EMNF là hình bình hành

b. Các đường thẳng AC, EF, MN đồng quy.

Lời giải:

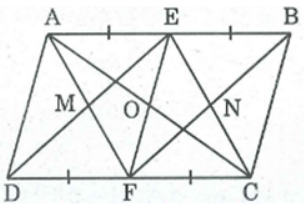
a. Xét tứ giác AECF, ta có:

AB // CD (gt)

Hay AE //CF

AE = 1/2 AB

AB = CD (tính chất hình bình hành)

Suy ra: AE = CF

Tứ giác AECF là hình bình hành (vì có một cặp cạnh đối diện song song và bằng nhau) ⇒ AF //CE hay EN // FM (1)

Xét tứ giác BFDE ta có:

AB // CD (gt) hay BE // DF

BE = 1/2 AB (gt)

DF = 1/2 CD (gt)

AB = CD (tính chất hình bình hành)

Suy ra: BE = DF

Tứ giác BFDE là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau) ⇒ BF//DE hay EM // FN (2)

Từ (1) và (2) suy ra tứ giác EMNF là hình bình hành (theo định nghĩa hình bình hành).

b. Gọi O là giao điểm của AC và EF

Tứ giác AECF là hình bình hành ⇒ OE = OF

Tứ giác EMFN là hình bình hành trên hai đường chéo cắt nhau tại trung điểm của mỗi đường.

Suy ra: MN đi qua trung điểm O của EF.

Vậy AC, EF, MN đồng quy tại O.

Bài 84 trang 90 SBT Toán 8 Tập 1: Hình dưới cho ABCD là hình bình hành. Chứng minh rằng:

a. EGFH là hình bình hành.

b. Các đường thẳng AC, BD, EF, GH đồng quy.

Lời giải:

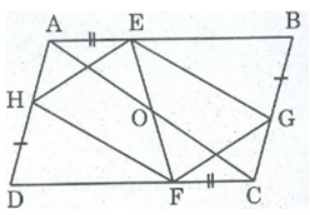
a. Xét ΔAEH và ΔCFG:

AE = CF (gt)

∠A = ∠C (tính chất hình bình hành)

AE = CF (vì AD = BC và DH = BG)

Do đó: ΔAEH = ΔCFG (c.g.c)

⇒ EH = FG

Xét ΔBEG và ΔDFH, ta có:

DH = BG (gt)

∠B = ∠D (tính chất hình bình hành)

BE = DF (vì AD = CD và AE = CF)

Do đó: ΔBEG = ΔDFH (c.g.c) ⇒ EG = FH

Suy ra: Tứ giác EGFH là hình bình hành (vì có các cặp cạnh đối bằng nhau)

b. Gọi O là giao điểm của AC và EF

Xét tứ giác AECF, ta có: AB // CD (gt) hay AE // CF

AE = CF (gt)

Suy ra: Tứ giác AECF là hình bình hành (vì có 1 cặp cạnh đối song song và bằng nhau)

⇒ O là trung điểm của AC và EF

Tứ giác ABCD là hình bình hành có O là trung điểm AC nên O cũng là trung điểm của BD.

Tứ giác EFGH là hình bình hành có O là trung điểm EF nên O cũng là trung điểm của GH.

Vậy AC, BD, EF, GH đồng quy tại O.

Bài 85 trang 90 SBT Toán 8 Tập 1: Cho hình hình hành ABCD. Qua C kẻ đường thẳng xy chỉ có một điểm chung C với hình bình hành. Gọi AA', BB', DD' là các đường vuông góc kẻ từ A, B, D đến đường thẳng xy. Chứng minh rằng AA' = BB' + DD'

Lời giải:

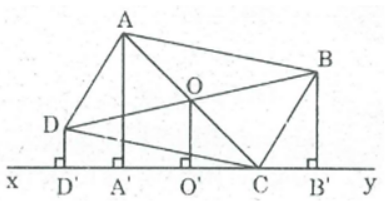
Gọi O là giao điểm của hai đường chéo AC và BD.

Kẻ OO' ⊥ xy

Ta có: BB' ⊥ xy (gt)

DD' ⊥ xy (gt)

Suy ra: BB // OO' // DD'

Tứ giác BB'D'D là hình thang .

OB = OD (t/chất hình bình hành)

Nên O'B' = O'D'

Do đó OO' là đường trung bình của hình thang BB'D'D

⇒ OO' = (BB' + DD') / 2 (tính chất đường trung hình hình thang) (1)

AA' ⊥ xy (gt)

OO' ⊥ xy (theo cách vẽ)

Suy ra: AA' // OO'

Trong ΔACA' tacó: OA = OC (tính chất hình bình hành)

OO' // AA' nên OO' là đường trung bình của ΔACA'

⇒ OO' = 1/2 AA' (tính chất đường trung bình của tam giác)

⇒ AA' = 2OO' (2)

Tử (1) và (2) suy ra: AA' = BB' + DD'

Bài 86 trang 90 SBT Toán 8 Tập 1: Cho hình bình hành ABCD và đường thẳng xy không có điểm chung với hình bình hành. Gọi là các đường vuông góc kẻ từ A, B, C, D đến đường thẳng xy.

Tìm mối liên hệ độ dài giữa AA', BB', CC', DD'

Lời giải:

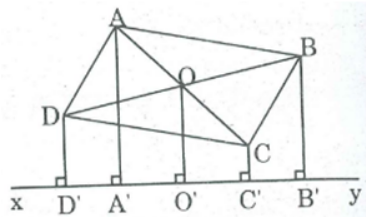
Gọi O là giao điểm của AC và BD

⇒ OA = OC, OB = OD (tính chất hình bình hành)

Kẻ OO' ⊥ xy

AA' ⊥ xy (gt)

CC' ⊥ xy (gt)

Suy ra: AA' // OO' // CC'

Tứ giác ACC'A' là hình thang có:

OA = OC (chứng minh trên)

OO' // AA' nên OO' là đường trung bình của hình thang ACC'A'.

⇒ OO' = (AA' + CC') / 2 (t/chất đường trung bình của hình thang) (1)

BB' ⊥ xy

DD' ⊥ xy (gt)

OO' ⊥ xy (gt)

Suy ra: BB'// OO' // DD'

Tứ giác BDD'B' là hình thang có:

OB = OD (Chứng minh trên)

OO' // BB' nên OO' là đường trung bình của hình thang BDD'B'.

⇒ OO' = (BB' + DD') / 2 (tính chất đường trung bình của hình thang) (2)

Bài 87 trang 90 SBT Toán 8 Tập 1: Cho hình bình hành ABCD có A = α > 90^o. Ở phía ngoài hình bình hành vẽ các tam giác đều ADP, ABE

a. Tính góc (EAF)

b. Chứng minh rằng tam giác CEF là tam giác đều.

Lời giải:

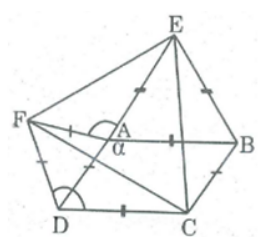
a. Vì ∠(BAD) + ∠(BAE) + ∠(EAF) + ∠(FAD) = 360^o

⇒ ∠(EAF) = 360^o – (∠(BAD) + ∠(BAE) + ∠(FAD) )

Mà ∠(BAD) = α^o (gt)

∠(BAE) = 60^o (ΔBAE đều)

∠(FAD) = 60^o (ΔFAD đều)

Nên ∠(EAF) = 360^o – (α^o + 60^o + 60^o) = 240^o – α

b. Ta có:

∠(BAD) + ∠(ADC) = 180^o (hai góc trong cùng phía bù nhau)

⇒ ∠(ADC) = 180^o - ∠(BAD) = 180^o – α

∠(CDF) = ∠(ADC) + ∠(ADF) = 180^o - α^o + 60^o = 240^o – α

Suy ra: ∠(CDF) = ∠(EAF)

Xét ΔAEF và ΔDCF: AF = DF ( vì ΔADF đều)

AE = DC (vì cùng bằng AB)

∠(CDF) = ∠(EAF) (chứng minh trên)

Do đó: ΔAEF = ΔDCF (c.g.c) ⇒ EF = CF (1)

∠(CBE) = ∠(ABC) + 60^o = 180^o – α + 60^o = 240^o – α

Xét ΔBCE và ΔDCF: BE = CD ( vì cùng bằng AB)

∠(CBE) = ∠(CDF) = 240^o – α

BC = DF (vì cùng bằng AD)

Do đó ΔBCE = ΔDCF (c.g.c) ⇒ CE = CF (2)

Từ (1) và (2) suy ra: EF = CF = CE

Vậy Δ ECF đều.

Bài 88 trang 90 SBT Toán 8 Tập 1: Cho tam giác ABC. Ở phía ngoài tam giác vẽ các tam giác vuông cân tại A là ABD, ACE. Vẽ hình bình hành ADIE. Chứng minh rằng:

a. IA = BC

b. IA ⊥ BC

Lời giải:

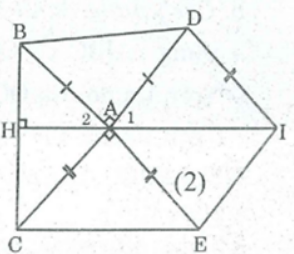
a. ∠(BAD) + ∠(BAC) + ∠(DAE) + ∠(EAC) = 360^o

∠(BAD) = 360^o, ∠(EAC) = 360^o

Suy ra: ∠(BAC) + ∠(DAE) = 180^o (1)

AE // DI (gt)

⇒ ∠(ADI) + ∠(DAE) = 180^o (2 góc trong cùng phía)

Từ (1) và (2) suy ra: ∠(BAC) = ∠(ADI)

Suy ra: ΔABC = ΔDAI (c.g.c) ⇒ IA = BC

b. ΔABC = ΔDAI (chứng minh trên) ⇒ ∠A₁= ∠B₁

Gọi giao điểm IA và BC là H.

Ta có: ∠A₁+ ∠(BAD) + ∠A₂= 180^o (kề bù)

Mà ∠(BAD) = 90^o (gt) ⇒ ∠A₁+ ∠A₂= 90^o

Trong ΔAHB ta có: ∠(AHB) + ∠B₁+ ∠A₂= 180^o

Suy ra ∠(AHB) = 90^o ⇒ AH ⊥ BC hay IA ⊥ BC