Bài II.1, II.2, II.3 trang 173 SBT Toán 9 Tập 1

---

Bài II.1, II.2, II.3 trang 173 SBT Toán 9 Tập 1

Bài 1 trang 173 Sách bài tập Toán 9 Tập 1: Tỉ số bán kính đường tròn nội tiếp và đường tròn ngoại tiếp một tam giác đều bằng

A. 1/3;     B. 1/2;

C. 1/√2;     D. 2.

Hãy chọn phương án đúng.

Lời giải:

Chọn đáp án B

Bài 2 trang 173 Sách bài tập Toán 9 Tập 1: Cho nửa đường tròn (O) đường kính AB. Trên nửa mặt phẳng bờ AB chứa nửa đường tròn, vẽ các tia tiếp tuyến Ax và By với nửa đường tròn. Gọi M là điểm thuộc nửa đường tròn, D là giao điểm của AM và By, C là giao điểm của BM và Ax, E là trung điểm của BD. Chứng minh rằng:

a) AC.BD = AB²;

b) ME là tiếp tuyến của nửa đường tròn.

Lời giải:

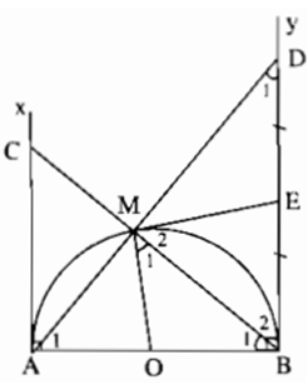
a) ∠B₁ = ∠D₁ (cùng phụ với ∠A₁).

ΔABC ∼ ΔBDA (g.g) suy ra

AB/BD = AC/AB, do đó AC.BD = AB₂.

b) Tam giác EBM cân nên ∠M₂ = ∠B₂. Suy ra ∠M₁ + ∠M₂ = ∠B₁ + ∠B₂ = 90^o, tức là ME ⊥ OM tại M. Vậy ME là tiếp tuyến của nửa đường tròn.

Bài 3 trang 173 Sách bài tập Toán 9 Tập 1: Cho đường tròn (O) và điểm A cố định trên đường tròn. Gọi xy là tiếp tuyến với đường tròn tại A. Từ một điểm M nằm trên xy, vẽ tiếp tuyến MB với đường tròn. Gọi H là trực tâm của tam giác MAB.

a) Chứng minh rằng ba điểm M, H, O thẳng hàng.

b) Tứ giác AOBH là hình gì?

c) Khi M di chuyển trên xy thì H di chuyển trên đường nào ?

Lời giải:

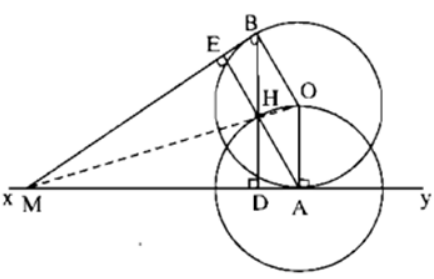
a) Gọi BD, AE là đường cao của ΔMAB. Ta có ΔMAE = ΔMBD (cạnh huyền – góc nhọn) nên ME = MD, ΔMHE = ΔMHD (cạnh huyền – cạnh góc vuông) nên ∠(EMH) = ∠(DMH). MH và MO đều là tia phân giác của góc AMB nên M, H, O thẳng hàng.

b) Tứ giác AOBH có BH // OA, AH // OB và OA = OB nên là hình thoi.

c) H cách A cố định một khoảng bằng OA không đổi nên H di chuyển trên đường tròn (A; AO).