Bài 14, 15, 16, 17 trang 64 SBT Toán 9 Tập 1

---

Bài 14, 15, 16, 17 trang 64 SBT Toán 9 Tập 1

Bài 14 trang 64 Sách bài tập Toán 9 Tập 1: a. Vẽ đồ thị của các hàm số sau trên cùng một mặt phẳng tọa độ:

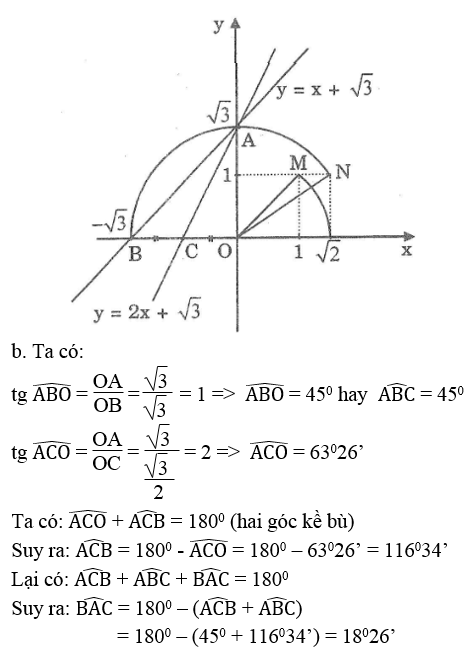
y = x + √3 (1)

y = 2x + √3 (2)

b. Gọi giao điểm của đường thẳng y = x + √3 với các trục Ox, Oy theo thứ tự là A, B và giao điểm của đường thẳng y = 2x + √3 với các trục Ox, Oy theo thứ tự là A, C. Tính các góc của tam giác ABC.

Lời giải:

a. *Vẽ đồ thị của hàm số y = x + √3

Cho x = 0 thì y = √3 . Ta có: A(0; √3 )

Cho y = 0 thì x + √3 = 0 => x = - √3 . Ta có: B(-√3 ; 0)

Cách tìm điểm có tung độ bằng √3 trên trục Oy:

- Dựng điểm M(1; 1). Ta có: OM = √2

- Dựng cung tròn tâm O bán kính OM cắt trục OX tại điểm có hoành độ bằng 2

- Dựng điểm N(1; √2 ). Ta có: ON = √3

- Vẽ cung tròn tâm O bán kính ON cắt trục Oy tại A có tung độ 3 cắt tia đối của Ox tại B có hoành độ -3

Đồ thị của hàm số y = x + √3 là đường thẳng AB.

*Vẽ đồ thị của hàm số y = 2x + √3

Cho x = 0 thì y = √3 . Ta có: A(0; √3 )

Cho y = 0 thì 2x + √3 = 0 => x = - √3/2 . Ta có: C(-√3/2 ; 0)

Đồ thị của hàm số y = 2x + √3 là đường thẳng AC.

Bài 15 trang 64 Sách bài tập Toán 9 Tập 1: Cho hàm số y = (m – 3)x

a. Với giá trị nào của m thì hàm số đồng biến? Nghịch biến?

b. Xác định giá trị của m để đồ thị của hàm số đi qua điểm A(1; 2)

c. Xác định giá trị của m để đồ thị của hàm số đi qua điểm B(1; -2)

d. Vẽ đồ thị của hai hàm số ứng với giá trị của m tìm được ở các câu b, c.

Lời giải:

Điều kiện: m – 3 ≠ 0 ⇔ m ≠ 3

a. *Hàm số đồng biến khi hệ số a = m – 3 > 0 ⇔ m > 3

Vậy với m > 3 thì hàm số y = (m – 3)x đồng biến.

*Hàm số nghịch biến khi hệ số a = m – 3 < 0 ⇔ m < 3

Vậy với m < 3 thì hàm số y = (m – 3)x nghịch biến.

b. Đồ thị của hàm số y = (m – 3)x đi qua điểm A(1; 2) nên tọa độ điểm A nghiệm đúng phương trình hàm số.

Ta có: 2 = (m – 3).1 ⇔ 2 = m – 3 ⇔ m = 5

vGiá trị m = 5 thỏa mãn điều kiện bài toán.

Vậy với m = 5 thì đồ thị hàm sô y = (m – 3)x đi qua điểm A(1; 2).

c. Đồ thị của hàm số y = (m – 3)x đi qua điểm B(1; -2) nên tọa độ điểm B nghiệm đúng phương trình hàm số.

Ta có: -2 = (m – 3).1 ⇔ -2 = m – 3 ⇔ m = 1

Giá trị m = 1 thỏa mãn điều kiện bài toán.

Vậy với m = 1 thì đồ thị hàm số y = (m – 3)x đi qua điểm B(1; -2)

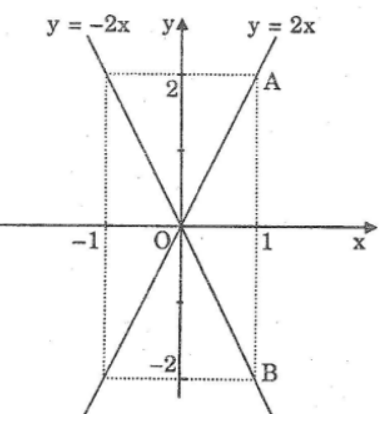
d. Khi m = 5 thì ta có hàm số: y = 2x

Khi m = 1 thì ta có hàm số: y = -2x

*Vẽ đồ thị của hàm số y = 2x

Cho x = 0 thì y = 0. Ta có: O(0; 0)

Cho x = 1 thì y = 2. Ta có: A(1; 2)

Đường thẳng OA là đồ thị hàm số y = 2x

*Vẽ đồ thị của hàm số y = -2x

Cho x = 0 thì y = 0. Ta có: O(0; 0)

Cho x = 1 thì y = -2. Ta có: B(1; -2)

Đường thẳng OB là đồ thị hàm số y = -2x

Bài 16 trang 64 Sách bài tập Toán 9 Tập 1: Cho hàm số y = (a – 1)x + a

a. Xác định giá trị của a để đồ thị của hàm số cắt trục tung tại điểm có tung độ bằng 2.

b. Xác định giá trị của a để đồ thị của hàm số cắt trục hoành tại điểm có hoành độ bằng -3.

c. Vẽ đồ thị của hai hàm số ứng với giá trị của a tìm được ở các câu a, b trên cùng hệ trục tọa độ Oxy và tìm tọa độ giao điểm của hai đường thẳng vừa vẽ được.

Lời giải:

a. Hàm số y = (a – 1)x + a (a ≠ 1) là hàm số bậc nhất có đồ thị hàm số cắt trục tung tại điểm có tung độ bằng y = 2 nên a = 2.

b. Hàm số y = (a – 1)x + a (a ≠ 1) là hàm số bậc nhất có đồ thị hàm số cắt trục hoành tại điểm có hoành độ x = -3 nên tung độ giao điểm này bằng 0.

Ta có: 0 = (a – 1)(-3) + a ⇔ -3x + 3 + a = 0

⇔ -2a = -3 ⇔ a = 1,5

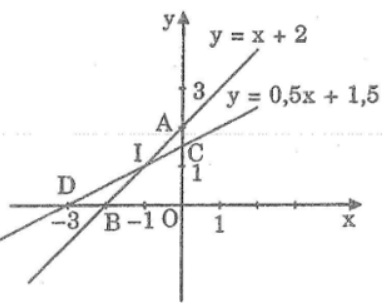
c. Khi a = 2 thì ta có hàm số: y = x + 2

Khi a = 1,5 thì ta có hàm số: y = 0,5x + 1,5

*Vẽ đồ thị của hàm số y = x + 2

Cho x = 0 thì y = 2. Ta có: A(0; 2)

Cho y = 0 thì x = -2. Ta có: B(-2; 0)

Đường thẳng AB là đồ thị hàm số y = x + 2

*Vẽ đồ thị hàm số y = 0,5x + 1,5

Cho x = 0 thì y = 1,5. Ta có: C(0; 1,5)

Cho y = 0 thì x = -3. Ta có: D(-3; 0)

Đường thẳng CD là đồ thị hàm số y = 0,5x + 1,5.

*Tọa độ giao điểm của hai đường thẳng:

Gọi I(x₁; y₁) là tọa độ giao điểm của hai đường thẳng.

Ta có: I thuộc đường thẳng y = x + 2 nên y₁ = x₁ + 2

I thuộc đường thẳng y = 0,5x + 1,5 nên y₁ = 0,5x₁ + 1,5

Suy ra: x₁ + 2 = 0,5x₁ + 1,5 ⇔ 0,5x₁= -0,5 ⇔ x₁ = -1

x₁ = -1 ⇒ y₁ = -1 + 2 = 1

Vậy tọa độ giao điểm của hai đường thẳng là I(-1; 1)

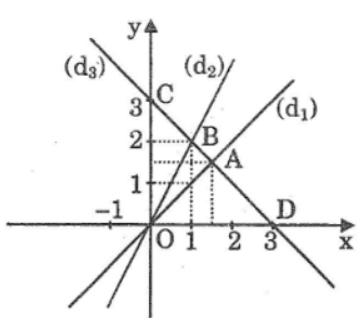
Bài 17 trang 64 Sách bài tập Toán 9 Tập 1: a. Vẽ trên cùng hệ trục tọa độ Oxy đồ thị các hàm số sau đây:

y = x (d₁)

y = 2x (d₂)

y = -x + 3 (d₃)

b. Đường thẳng (d₃) cắt đường thẳng (d₁) và (d₂) theo thứ tự tại A, B. Tìm tọa độ của các điểm A, B.

Lời giải:

a. *Vẽ đồ thị của hàm số y = x

Cho x = 0 thì y = 0

Cho x = 1 thì y = 1

Đồ thị hàm số y = x là đường thẳng đi qua gốc tọa độ O(0; 0) và điểm (1; 1)

*Vẽ đồ thị hàm số y = 2x

Cho x = 0 thì y = 0

Cho x = 1 thì y = 2

Đồ thị hàm số y = 2x là đường thẳng đi qua gốc tọa độ O(0; 0) và điểm (1;2)

*Vẽ đồ thị của hàm số y = -x + 3

Cho x = 0 thì y = 3. Ta có điểm (0; 3)

Cho y = 0 thì x = 3. Ta có điểm (3; 0)

Đồ thị hàm số y = -x + 3 là đường thẳng đi qua hai điểm (0; 3) và (3; 0)

b. *Gọi A(x₁; y₁), B(x₂; y₂) lần lượt là tọa độ giao điểm của đường thẳng (d₃) với hai đường thẳng (d₁), (d₂)

Ta có: A thuộc đường thẳng y = x nên y₁ = x₁

A thuộc đường thẳng y = -x + 3 nên y₁ = -x₁ + 3

Suy ra: x₁ = -x₁ + 3 ⇔ 2x₁ = 3 ⇔ x₁ = 1,5

x₁ = 1,5 ⇒ y₁ = 1,5

Vậy tọa độ giao điểm của hai đường thẳng (d₁) và (d₂) là A(1,5; 1,5)

Ta có: 2x₂ = -x₂ + 3 ⇔ 3x₂ = 3 ⇔ x₂ = 1

x₂ = 1 ⇒ y₂ = 2

Vậy tọa độ giao điểm của hai đường thẳng (d₂) và (d₃) là B(1; 2).