Bài III.2, III.3, III.4, III.5, III.6 trang 115 SBT Toán 9 Tập 2
Bài III.2, III.3, III.4, III.5, III.6 trang 115 SBT Toán 9 Tập 2
Bài 2 trang 115 Sách bài tập Toán 9 Tập 2: Cho đường tròn tâm O bán kính R và điểm M ở ngoài đường tròn đó. Qua điểm M kẻ hai tiếp tuyến MA, MB và cắt tuyến MCD với đường tròn (O), trong đó điểm C ở giữa hai điểm M, D. Đường thẳng qua điểm C và vuông góc với OA cắt AB tại H. Gọi I là trung điểm của dây CD. Chứng minh HI song song với AD.
Lời giải:
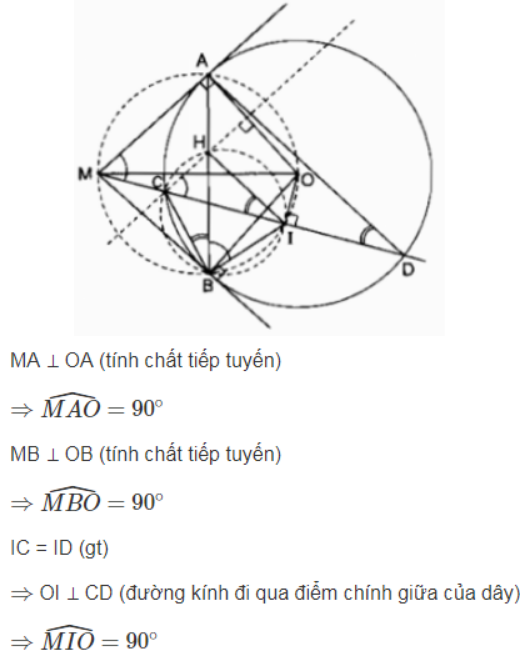
A, B, I nhìn MO cố định dưới một góc bằng 90° nên A, B, I nằm trên đường tròn bán kính MO.

B và C cùng nằm trên một nửa mặt phẳng bờ chứa đường HI tạo với HI một góc bằng nhau nên tứ giác BCHI nội tiếp.

Bài 3 trang 115 Sách bài tập Toán 9 Tập 2: Hãy chỉ ra phương án mà em cho là đúng.
Góc nội tiếp là góc:
(A) có đỉnh nằm trên đường tròn.
(B) có hai cạnh là hai giây của đường tròn.
(C) có hai đỉnh là tâm đường tròn và có hai cạnh là hai bán kính.
(D) có hai cạnh là hai dây của đường tròn đó và chỉ có một đầu mút chung.
Lời giải:
Chọn (D) có hai cạnh là hai dây của đường tròn đó và chỉ có một đầu mút chung.
Bài 4 trang 115 Sách bài tập Toán 9 Tập 2: Một đường tròn là đường tròn nội tiếp nếu có:
(A) đi qua các đỉnh của một tam giác.
(B) tiếp xúc với các đường thẳng chứa các cạnh của một tam giác.
(C) tiếp xúc với các cạnh của một tam giác.
(D) nằm trong một tam giác.
Lời giải:
Chọn (C) tiếp xúc với các cạnh của một tam giác.
Bài 5 trang 115 Sách bài tập Toán 9 Tập 2: Một tứ giác là tứ giác nội tiếp nếu
(A) có hai đỉnh cùng nhìn một cạnh dưới hai góc bằng nhau.
(B) có 4 góc bằng nhau.
(C) có 4 cạnh bằng nhau.
(D) có các cạnh tiếp xúc với đường tròn.
Lời giải:
Chọn (A) có hai đỉnh cùng nhìn một cạnh dưới hai góc bằng nhau.
Bài 6 trang 115 Sách bài tập Toán 9 Tập 2: Quỹ tích các điểm M nhìn đoạn thẳng AB dưới một góc 120° là
(A) một đường tròn đi qua hai điểm A, B.
(B) một đường thẳng song song với AB.
(C) một cung chứa góc 120°dựng trên hai điểm A, B.
(D) hai cung chứa góc 120° (đối xứng nhau) dựng trên hai điểm A, B).
Lời giải:
Chọn (D) hai cung chứa góc 120° (đối xứng nhau) dựng trên hai điểm A, B).

