Bài 41, 42, 43, 44 trang 58 SBT Toán 9 Tập 2

---

Bài 41, 42, 43, 44 trang 58 SBT Toán 9 Tập 2

Bài 41 trang 58 Sách bài tập Toán 9 Tập 2: Tìm hai số u và v trong mỗi trường hợp sau:

a. u +v =14, uv =40     b. u +v =-7, uv =12

c. u +v =-5, uv =-24     d. u +v =4, uv =19

e. u – v =10, uv =24     f. u² + v² =85,uv =18

Lời giải:

a) Hai số u và v với u +v =14 và uv =40 nên nó là nghiệm của phương trình x² -14x + 40=0

Δ’= (-7)² – 1.40=49 -40 =9 > 0

√Δ' = √9 =3

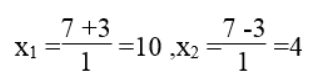
Vậy u=10, v=4 hoặc u = 4, v = 10

b. Hai số u và v với u +v =-7 và uv =12 nên nó là nghiệm của phương trình x² +7x + 12=0

Δ= (7)² – 4.1.12=49 -48=1 > 0

√Δ =√1 =1

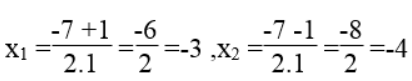
Vậy u=-3,v=-4 hoặc u=-4,v=-3

c. Hai số u và v với u +v =-5 và uv =-24 nên nó là nghiệm của phương trình x² +5x -24 =0

Δ= (5)² – 4.1.(-24)= 25 +96=121 > 0

√Δ = √121 =11

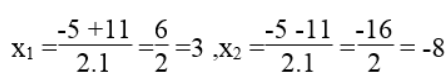
Vậy u = 3, v = -8 hoặc u = -8, v = 3

d. Hai số u và v với u +v =4 và uv =19 nên nó là nghiệm của phương trình x² - 4x +19 = 0

Δ’= (-2)² – 1.19= 4 - 19=-15 < 0

Phương trình vô nghiệm nên không có giá trị nào của u và v thỏa mãn điều kiện bài toán

e. Hai số u và v với u – v =10 suy ra : u + (- v) = 10 và uv = 24 suy ra u(-v) = -24 nên nó là nghiệm của phương trình x² -10x -24 =0

Δ’= (-5)² – 1.(-24)= 25 +24=49 > 0

√Δ' = √49 =7

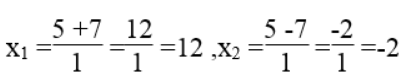
Vậy u = 12 , -v = -2 hoặc u = -2, -v = 12 suy ra u = 12 , v = 2 hoặc u = -2 , v = -12

f. Hai số u và v với u² + v² =85 và uv =18 suy ra : u²v²=324 nên u² và v² là nghiệm của phương trình x² -85x +324 =0

Δ= √(-85)² – 4.1.324= 7225 – 1296=5929 > 0

√Δ = √2959 =77

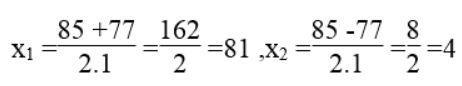
Ta có: u² =81 ,v² =4 suy ra: u =±9 ,v=± 2

hoặc u² =4 ,v² =81 suy ra: u =±2 ,v=± 9

Vậy nếu u=9 thì v=2 hoặc u=-9 ,v=-2

nếu u=2 thì v=9 hoặc u= -2 ,v=-9

Bài 42 trang 58 Sách bài tập Toán 9 Tập 2: Lập phương tình có hai nghiệm là hai số được cho mỗi trường hợp sau:

a. 3 và 5    b.-4 và 7

c. -5 và 1/3    d.1,9 và 5,1

e. 4 và 1 -√2    f.3 - √5 và 3 + √5

Lời giải:

a) Hai số 3 và 5 là nghiệm của phương trình:

(x -3)(x -5) = 0 ⇔ x² -3x -5x +15 =0 ⇔ x² -8x +15 =0

b. Hai số 3 và 5 là nghiệm của phương trình:

(x +4)(x -7) = 0 ⇔ x² +4x -7x -28 =0 ⇔ x² -3x -28 =0

c. Hai số -5 và 1/3 là nghiệm của phương trình:

(x +5)(x -1/3 )=0 ⇔ x² +5x -1/3 x -5/3 =0 ⇔ 3x² +14x - 5 =0

d. Hai số 1,9 và 5,1 là nghiệm của phương trình:

(x - 1,9)(x -5,1)=0 ⇔ x² - 1,9x - 5,1x + 9,69 = 0

⇔ x² -7x + 9,69 = 0

e. Hai số 4 và 1 -√2 là nghiệm của phương trình:

(x - 4)[x –(1 -√2 )] =0 ⇔ (x -4)(x -1 +√2 ) =0

⇔ x² - x +√2 x -4x +4 - 4√2 =0

⇔ x² – (5 -√2 )x +4 - 4√2 =0

f. Hai số 3 - √5 và 3 + √5 là nghiệm của phương trình:

[x – (3 - √5 )][ x – (3 + √5 )] = 0

⇔ x² – (3 + √5 )x - (3 - √5 )x +(3+ √5 )(3 - √5 ) =0

⇔ x² -6x +4 =0

Bài 43 trang 58 Sách bài tập Toán 9 Tập 2: Cho phương trình x² + px – 5 = 0 có hai nghiệm x₁ và x². Hãy lập phương trình có hai nghiệm là hai số được cho trong mỗi trường hợp sau:

a. –x₁ và –x₂    b. 1/x₁ và 1/x₂

Lời giải:

a) Phương trình x²+px -5=0 có hai nghiệm x₁ và x₂ nên theo hệ thức vi-ét ta có:

x₁ + x₂ = -p/1 = -p ; x₁x₂ =-5/1 =-5 (1)

Hai số –x₁ và –x₂ là nghiệm của phương trình:

[x – (-x₁)] [x – (-x₂)] =0

⇔ x₂ – (-x₁x) – (-x₂x) + (-x₁)(-x₂) =0

⇔ x₂ + (x₁ + x₂x + x₁x₂) =0 (2)

Từ (1) và (2) ta có phuơng trình cần tìm là x² – px -5 =0

Bài 44 trang 58 Sách bài tập Toán 9 Tập 2: Cho phương trình x² -6x +m=0

Tính giá trị của m biết rằng phương trình có hai nghiệm x₁,x₂ thỏa mãn điều kiện x₁ –x₂ =4

Lời giải:

Phương trình x² - 6x + m = 0 có hai nghiệm x₁ và x₂ nên theo hệ thức Vi-ét ta có:

x₁ + x₂ =-(-6)/1 = 6

Kết hợp với điều kiện x₁ – x₂ =4 ta có hệ phương trình :

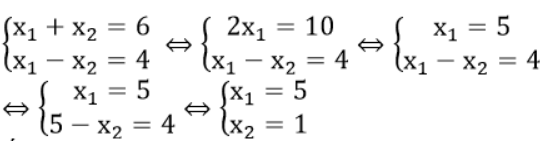
Áp dụng hệ thức vi-ét vào phương trình x² -6x +m=0 ta có:

x₁x₂ = m1 = m . Suy ra : m = 5.1 = 5

Vậy m =5 thì phương trình x² -6x +m=0 có hai nghiệm x₁ và x₂ thỏa mãn điều kiện x₁ – x₂ =4