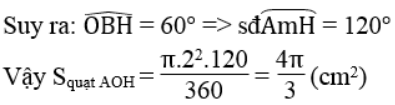Bài 71, 72 trang 113 SBT Toán 9 Tập 2

---

Bài 71, 72 trang 113 SBT Toán 9 Tập 2

Bài 71 trang 113 Sách bài tập Toán 9 Tập 2: Trong tam giác đều ABC ,vẽ những cung tròn đi qua tâm của tam giác và từng cặp đỉnh của nó. Cho biết cạnh tam giác bằng a,tính diện tích hình hoa thị gạch sọc

Lời giải:

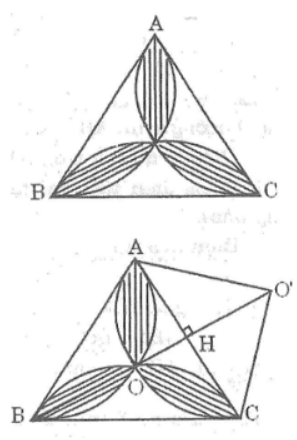
Gọi O là tâm của tam giác đều ABC

Ta có: OA =OB=OC

Vì ABC là tam giác đều nên AO,BO , CO là tia phân giác của góc A , góc B ,góc C trong ΔOAC ta có:

Bài 72 trang 113 Sách bài tập Toán 9 Tập 2: Cho tam giác ABC vuông ở A và đường cao AH.Vẽ đường tròn tam O đường kính AB.Biết BH = 2cm và HC = 6cm.Tính:

a.Diện tích hình tròn (O)

b.Tổng diện tích hai hình viên phân AmH và BnH (ứng với các cung nhỏ)

c.diện tích hình quạt tròn AOH (ứng với các cung nhỏ AH)

Lời giải:

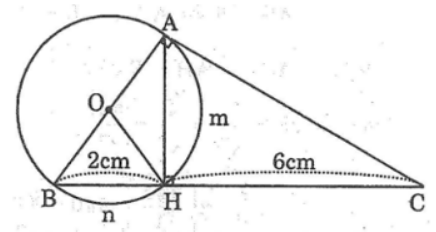
a) Trong tam giác ABC vuông tại A nên ta có:

AB² = BH.BC =2.(2+6)=2.8=16

suy ra AB = 4cm

Diện tích hình tròn tâm (O) là :

S=π.(AB/2 )² = π.(4/2 )² = 4π (cm²)

b) Trong tam giác vuông ABC có:

AH² = HB.HC =2.6=12

Suy ra: AH =2.√3 cm

Diện tích tam giác AHB:

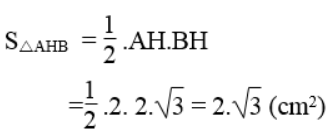
Tổng diện tích hai hình viên phân AmH và BnH bằng diện tích nửa hình tròn tâm O trừ diện tích tam giác AHB co:

S = 2π - 2.√3 = 2(π - √3 ) (cm²)

c) Ta có AB=4cm ⇒ OB =2cm

Tam giác OBH có OB = OH =HB = 2cm nên tam giác OBH đều