Chứng minh rằng nếu khối đa diện có các mặt là tam giác thì số mặt phải là số chẵn

Bài 1: Khái niệm về khối đa diện

Haylamdo biên soạn và sưu tầm lời giải Bài 1 trang 7 sgk Hình Học 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Bài 1 (trang 7 sgk Hình Học 12 nâng cao): Chứng minh rằng nếu khối đa diện có các mặt là tam giác thì số mặt phải là số chẵn. Hãy chỉ ra những khối đa diện như thế với số mặt bằng 4, 6, 8, 10.

Lời giải:

- Giải sử khối đa diện đã cho có M mặt và C cạnh.

Vì mỗi mặt có 3 cạnh nên M mặt có 3M cạnh, nhưng mỗi cạnh lại là cạnh chung cho 2 mặt nên có 2C = 3M, suy ra M chẵn. vậy nếu khối đa diện có các mặt làm tam giác thì số mặt phải là số chẵn.

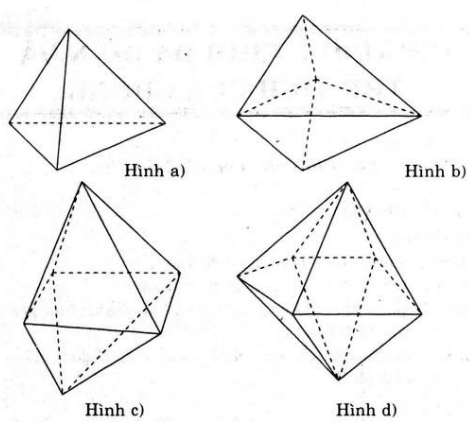
- Khối a) khối tứ diện có 4 mặt là tam giác.

- Hình b) khối 6 mặt là tam giác.

- Hình c) khối 8 mặt là tam giác.

- Hình d) khối 10 mặt là tam giác