Chứng minh rằng phép vị tự biến một đường thẳng a thành đường thẳng a’

Bài 3: Phép vi tự và sự đồng dạng của các khối đa diện. Các khối đa diện đều

Haylamdo biên soạn và sưu tầm lời giải Bài 11 trang 20 sgk Hình Học 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Bài 11 (trang 20 sgk Hình Học 12 nâng cao): Chứng minh rằng phép vị tự biến một đường thẳng a thành đường thẳng a’ song song a thành đường thẳng a’. hơn nữa (α) thành một mặt phẳng (α') song song hoặc trùng với α.

Lời giải:

- Do phép vị tự biến ba điểm thằng hành thành 3 điểm thằng hàng nên nó biến đường thẳng a thành a’. Hơn nữa a’ song song hoặc trùng với a

Thật vậy, trên a lấy điểm A, B; Giả sử V_0,k biến A thành A’ biến B thành B’.

Ta có:

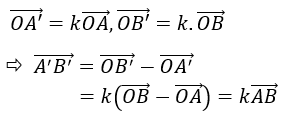
- Trường hợp 1: k = 1 và O ∈ a thì A’B’ = AB hay a = a’.

- Trường hợp 2: k ≠ 1 và O ∉ a thì A’B’ // AB hay a’ // a

Phép vị tự V_0,k biến đường thẳng thành đường thẳng song song hoặc trùng với nó nên biến hai đường thẳng cắt nhau thành hai đường thẳng cắt nhau. Vậy nó biến mp(α) thành mặt phẳng (α'). Hơn nữa mp(α') song song hoặc trùng với mp(α). Thật vậy:

- Nếu O ∈ (α) thì V_0,k biến A ∈(α) thành A’ sao cho OA'→=kOA→.

=> A'∈ OA hay A' ∈ mp(α) suy ra mp(α') = mp(α).

- Nếu k =1 thì V_(O,1)(A) = A’ hay 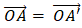⇒ A ≡ A'

Vậy qua V_(0,k) biến mp (α) thành mp(α') = mp(α).

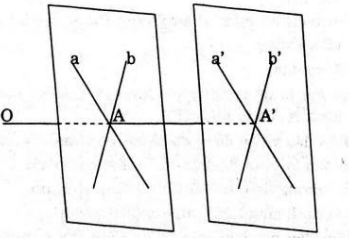
- Nếu O ∈ mp(α) và k ≠ 1. Trên mp(α) lấy hai đường thẳng a, b cắt nhau tại I.

Qua phép vị tự tâm O tỉ số k :

      + Biến hai đường thẳng a, b thành 2 đường thẳng a’, b’ song song hoặc trùng với a,b

      + Biến giao điểm I thành điểm I’ là giao điểm của hai đường thẳng a’ và b’.

      + Biến mp (α) thành mp(α’) chứa hai đường thẳng a’và b’.

Suy ra, mp(α) // mp (α’).