Chứng minh rằng: Tâm các mặt của khối lập phương cho trước là các đỉnh của một khối tám mặt đều
Bài 3: Phép vi tự và sự đồng dạng của các khối đa diện. Các khối đa diện đều
Haylamdo biên soạn và sưu tầm lời giải Bài 14 trang 20 sgk Hình Học 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.
Bài 14 (trang 20 sgk Hình Học 12 nâng cao): Chứng minh rằng:
a) Tâm các mặt của khối lập phương cho trước là các đỉnh của một khối tám mặt đều.
b) Tâm các mặt của một khối tám mặt đều cho trước là các đỉnh của khối lập phương.
Lời giải:
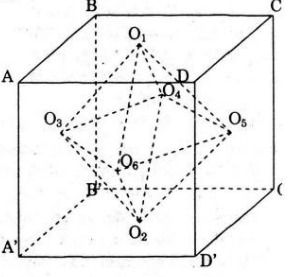
a) Xét khối lập phương ABCD.A’B’C’D’ cạnh a. Gọi O1, O2,O3,O4,O5,O6 lần lượt là tâm của các mặt phẳng ABCD, A’B’C’D’, ABB’A’, BCC’B’, CDD’C’, DAA’D.
Ta có: O1 là trung điểm của BD, O3 là trung điểm của A’B’ nên:
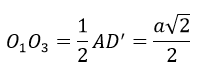
Tương tự: O1O4 = O1O5 = O1O6 = O3O4 = O4O5 = O5O6 = O1O6 = O3O4 = O4O5 = O5O6 = O6O3 = O2O3 = O2O4 = O2O5 = O2O6 = (a√2)/2
Do đó, các tam giác O1O3O6; O1O6O5; O1O5O4; O1O3O4; O2O3O6; O2O6O5; O2O5O4; O2O3O4 là các tam giác đều cạnh
Chúng làm thành khối tám mặt đều (đpcm).
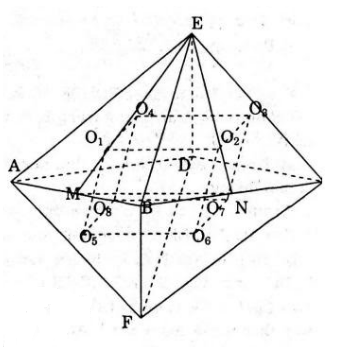
b) Xét khối tám mặt đều ABCDEF. Gọi O1, O2,O3,O4,O5,O6, O7, O8 lần lượt là trọng tâm của các mặt EAB, EBC, ECD, EDA, FAB, FBC, FCD, FDA.
- Gọi M, N lần lượt là trung điểm của AB, BC.
Ta có: O1,O2 là trọng tâm ΔEAB, EBC nên:
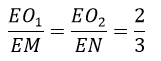
=> O1 O2 // MN
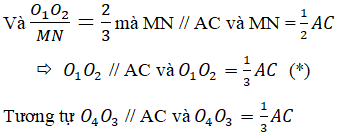
=> O1 O2 // O3 O4 và O1 O2 = O3 O4
=> Tứ giác O1 O2 O3 O4 là hình bình hành.
Lại có: O1 O4 // BD, O1 O4=BD/3 kết hợp (*) và lưu ý rằng.
AC = DB, AC ⊥ BD => O1 O2=O1 O4, O1 O2 ⊥ O1 O4 nên tứ giác O1 O2 O3 O4 là hình vuông.
- Hoàn toàn tương ứng ta có: O1 O2 O6 O5,O2 O3 O7 O6,O3 O4,O8 O7,O4 O1 O5 O8,O5 O6 O7 O8 là các hình vuông.
Vậy O1, O2,O3,O4,O5,O6, O7, O8 là các đỉnh của một khối lập phương.

