Tính diện tích các hình phẳng bởi giới hạn. Đồ thị hàm số y=x^2-4
Bài 5: Ứng dụng tích phân để tính diện tích hình phẳng
Haylamdo biên soạn và sưu tầm lời giải Bài 28 trang 167 sgk Giải Tích 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.
Bài 28 (trang 167 sgk Giải Tích 12 nâng cao): Tính diện tích các hình phẳng bởi giới hạn.
a) Đồ thị hàm số y=x2-4;y=-x2-2x và hai đường thẳng x = -3, x =- 2.
b) Đồ thị hàm số y=x2-4 và y=-x2-2x
c) Đồ thị hàm số y=x3-4x, trục hoành, đường thẳng x = -2 và đường thẳng x = 4.
Lời giải:
a) Dựa vào hình vẽ ta thấy diện tích phẳng cần tìm là:
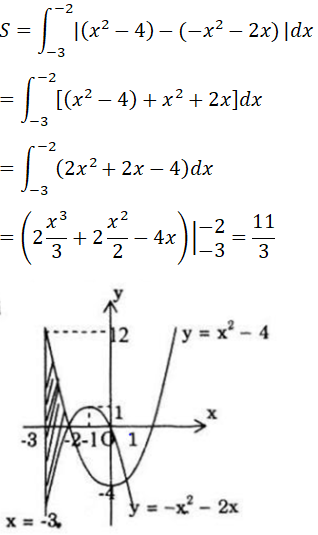
Chú ý: ở câu này, nếu không vẽ hình thì phải chứng tỏ rằng ∀x ∈(-3; -2) thì (x4-4)-(x2-2x) ≥ 0 để páp được giá trị tuyệt đối.
b) Phương trình hoành độ giao điểm đồ thị hai hàm số đã cho là:
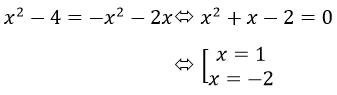
Dựa vào hình vẽ ở câu a ta có:
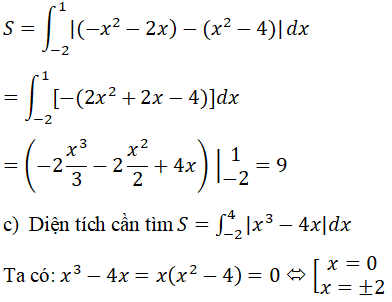
Ta có bảng xét dấu sau:
| x | -∞ | -2 | 0 | 2 | +∞ | ||||
| x | - | | | - | 0 | + | | | + | ||
| x2 - 4 | + | 0 | - | | | - | 0 | + | ||
| x(x2 - 4 ) | - | 0 | + | 0 | - | 0 | + |