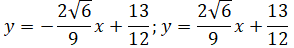Cho hàm số y=x^4-2mx^2+2m a) Tìm các giá trị của m sao cho hàm số có 3 cực trị

Luyện tập (trang 44-45)

Haylamdo biên soạn và sưu tầm lời giải Bài 48 trang 45 sgk Giải Tích 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Bài 48 (trang 45 sgk Giải Tích 12 nâng cao): Cho hàm số y=x⁴-2mx²+2m

a) Tìm các giá trị của m sao cho hàm số có 3 cực trị.

b) Khảo sát và vẽ đồ thị của hàm số với m=1/2. Viết Phương trình tiếp tuyến của đồ thị tại 2 điểm uốn.

Lời giải:

a) Ta có y'=4x³-4mx=4x(x²-m)

Để hàm số đã cho có 3 cực trị thì Phương trình y’=0 có 3 nghiệm phân biệt.

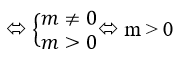
Vậy với m > 0 thì hàm số đã cho có 3 điểm cực trị.

b) Với m=1/2 ta có y=x⁴-x²+1

TXĐ: R

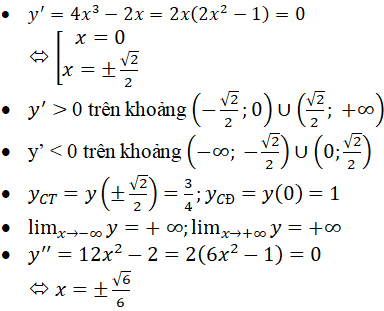
Bảng xét dấu y’’

Bảng biến thiên

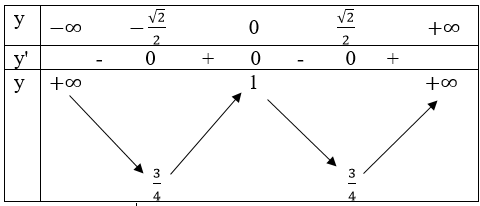
Đồ thị đi qua (0; 1)

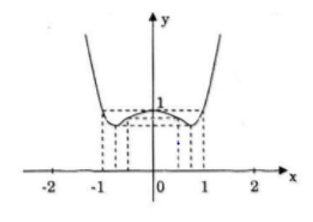
- y=x⁴-x²+1

Hàm số có 2 điểm uốn là

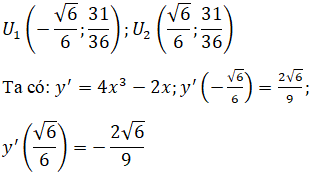
Phương trình tiếp tuyến tại điểm uốn

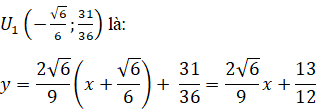
Phương trình tiếp tuyến tại điểm uốn

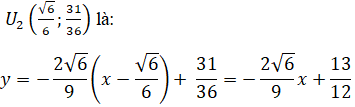
Vậy 2 phương trình tiếp tuyến tại điểm uốn là: