Chứng minh rằng đồ thị hàm số y=a^x và y=(1/a)^x đối xứng với nhau qua trục tung

Luyện tập (trang 117-118)

Haylamdo biên soạn và sưu tầm lời giải Bài 60 trang 117 sgk Giải Tích 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Bài 60 (trang 117 sgk Giải Tích 12 nâng cao):

a) Chứng minh rằng đồ thị hàm số y=a^x và y=(1/a)^x đối xứng với nhau qua trục tung.

b) Chứng minh rằng đồ thị của hai hàm số y=log_a⁡x và y=log_1/a⁡x đối xứng nhau qua trục hoành.

Lời giải:

a) Gọi (C₁) và (C₂) lần lượt là đồ thị của các hàm số y=a^x và y=(1/a)^x.

Lấy điểm M(x₀; y₀) là một điểm bất kì thuộc đồ thị (C₁). Khi đó điểm đối xứng với M qua trục tung là M'(-x₀;y₀)

Ta có: M ∈(C₁ ) <=> y₀=a^x₀

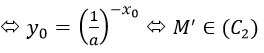
Điều đó chứng tỏ (C₁) và (C₂ )đối xứng nhau qua trục tung.

b) Chứng minh tương đương bài a, chú ý điểm đối xứng với M(x₀;y₀ ) qua trục hoành là điểm M'(x₀; -y₀)

M ∈(C₁ )<=> y₀=log_a⁡x₀ <=> y₀=-log^1/a⁡x₀ <=> -y₀=log_1/a⁡x₀ <=> M'∈(C₂)