Chứng minh rằng tâm của các mặt của hình tứ diện đều là các đỉnh

Toán lớp 12 Bài 2: Khối đa diện lồi và khối đa diện đều

Bài 3 (trang 18 SGK Hình học 12): Chứng minh rằng tâm của các mặt của hình tứ diện đều là các đỉnh của một tứ diện đều.

Lời giải:

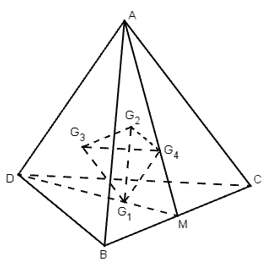
Xét tứ diện đều A.BCD cạnh bằng a. Gọi G₁, G₂, G₃ và G₄ lần lượt là tâm của các tam giác BCD, ACD, ABD và ABC.

Gọi M là trung điểm của BC.

Xét tam giác AMD có:

Tương tự ta có: G₁G₂ =G₂G₃ = G₃G₄ = G₁G₃ = G₁G₄ = G₂G₄ =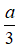

Tâm các mặt của tứ diện đều ABCD tạo thành tứ diện G₁G₂G₃G₄ có độ dài mỗi cạnh là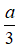

Vậy tứ diện G₁G₂G₃G₄ là tứ diện đều.