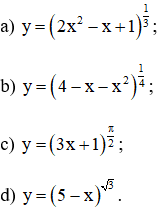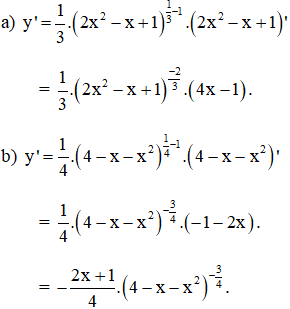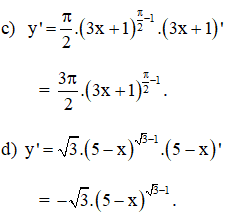Giải Toán 12 Bài 1: Lũy thừa
Trả lời câu hỏi Toán 12 Giải tích Bài 1 trang 49: Tính (1,5)4; ((-2)/3)3; (√3)5.
Lời giải:
(1,5)4 = 5.0625; ((-2)/3)3=(-8)/27; (√3)5 = 9√3
Trả lời câu hỏi Toán 12 Giải tích Bài 1 trang 50: Dựa vào đồ thị của các hàm số y = x3 và y = x4 (H.26, H.27), hãy biện luận theo b số nghiệm của các phương trình x3 = b và x4 = b.
Lời giải:
Số nghiệm của phương trình x3 = b là số giao điểm của hai đồ thị hàm số y = b và y = x3.
Dựa vào H26 ta có đồ thị hàm số y = x3 luôn cắt đường thẳng y = b tại một điểm duy nhất với mọi b nên phương trình x3 = b luôn có nghiệm duy nhất với mọi b.
Số nghiệm của phương trình x4 = b (1) là số giao điểm của hai đồ thị hàm số y = b và y = x4. Dựa và hình 27 ta có:
+ Với b < 0 hai đồ thị hàm số trên không giao nhau, vậy phương trình (1) vô nghiệm.
+ Với b = 0, hai đồ thị hàm số tiếp xúc nhau tại (0,0), vậy phương trình (1) có nghiệm duy nhất x = 0.
+ Với b > 0, hai đồ thị hàm số cắt nhau tại hai điểm phân biết, vậy phương trình (1) có hai nghiệm phân biệt.
Trả lời câu hỏi Toán 12 Giải tích Bài 1 trang 52: Chứng minh tính chất n√a . n√b = n√ab.
Lời giải:
Đặt n√a = x, n√b = y. Khi đó: xn = a, yn = b.
Ta có (xy)n = xn.yn = a.b. Vậy xy là căn bậc n của ab.
Suy ra n√ab = xy = n√a.n√b
Trả lời câu hỏi Toán 12 Giải tích Bài 1 trang 54: Hãy nhắc lại các tính chất của lũy thừa với số mũ nguyên dương.
Lời giải:
Các tính chất về đẳng thức
1. am. an = a(m+n)
2. am : an = a(m-n) (m ≥ n).
3. (am)n = amn
4.(a/b)m = am / bm (b ≠ 0)
5. (ab)m = am.bm
Các tính chất về bất đẳng thức
Với a > 1 thì am > an ⇔ m > n.
Với 0 < a < 1 thì am > an ⇔ m < n.
0 < a < b thì am > bm
Giải Toán 12 Bài 2: Hàm số lũy thừa
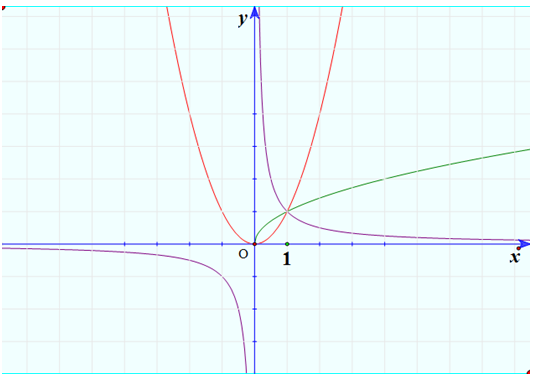
Trả lời câu hỏi Toán 12 Giải tích Bài 2 trang 57: Vẽ trên cùng một hệ trục tọa độ đồ thị của các hàm số sau và nêu nhận xét về tập xác định của chúng: y = x^2, y = x^(1/2), y = x^(-1).
Lời giải:
Đồ thị của hàm số y = x2: đường màu đỏ.
Đồ thị của hàm số y = x(1/2): đường màu xanh.
Đồ thị của hàm số y = x(-1) đường màu tím.
Ta có:
Tập xác định của hàm số y = x2 là R.
Tập xác định của hàm số y = x(1/2) là [0,+∞).
Tập xác định của hàm số y = x(-1)là R\{0}.
Trả lời câu hỏi Toán 12 Giải tích Bài 2 trang 57: Tính đạo hàm của các hàm số:
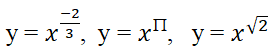
Lời giải:
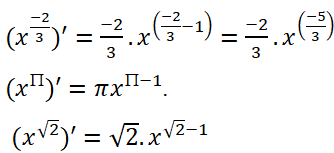
Trả lời câu hỏi Toán 12 Giải tích Bài 2 trang 58: Tính đạo hàm của hàm số y = (3x2 – 1)(-√2).
Lời giải:
y’= [(3x2 – 1)(-√2)]'
= -√2.(3x2 – 1)(-√2-1).(3x2 – 1)'
= -√2.(3x2 – 1)(-√2-1).6x
= -6√2 x.(3x2 – 1)(-√2-1).
Bài 1 (trang 60 SGK Giải tích 12): Tìm tập xác định của các hàm số:
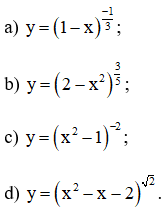
Lời giải:
a) Hàm số 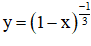 xác định
xác định
⇔ 1 – x > 0
⇔ x < 1.
Vậy tập xác định D = (-∞; 1).
b) Hàm số 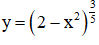 xác định
xác định
⇔ 2 – x2 > 0
⇔ x2 < 2
⇔ -√2 < x < √2.
Vậy tập xác định D = (-√2; √2).
c) Hàm số y = (x2 – 1)-2 xác định khi và chỉ khi:
x2 - 1 ≠ 0 ⇔ x2 ≠ 1 ⇔ x ≠ ±1
Vậy tập xác định của hàm số là D = R\ {-1; 1}.
d) Hàm số 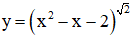 xác định
xác định
⇔ x2 – x – 2 > 0
⇔ (x + 1)(x – 2) > 0
⇔ x < -1 hoặc x > 2
Vậy tập xác định D = (-∞; -1) ∪ (2; +∞).
Kiến thức áp dụng
1. Khi xét lũy thừa với số mũ 0 hoặc số mũ nguyên âm thì cơ số phải khác 0.
2. Khi xét lũy thừa với số mũ không nguyên thì cơ số phải dương.
Bài 2 (trang 61 SGK Giải tích 12): Tính đạo hàm của các hàm số:
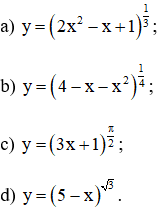
Lời giải:
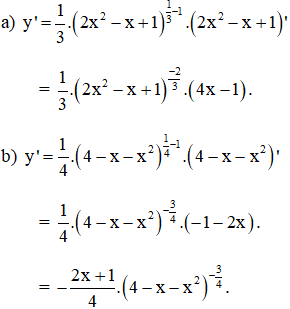
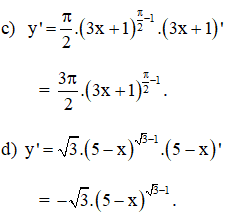
Kiến thức áp dụng
+ Đạo hàm của hàm số y = uα là: y' = (uα)' = α.uα - 1.u'



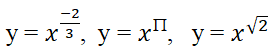
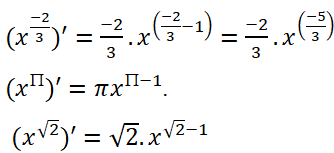
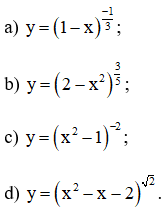
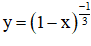 xác định
xác định 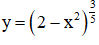 xác định
xác định 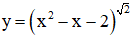 xác định
xác định