Giáo án Toán 12 Bài 2: Công thức xác suất toàn phần và công thức Bayes - Chân trời sáng tạo
Giáo án Toán 12 Bài 2: Công thức xác suất toàn phần và công thức Bayes - Chân trời sáng tạo
Chỉ từ 500k mua trọn bộ Kế hoạch bài dạy (KHBD) hay Giáo án Toán 12 Chân trời sáng tạo (cả năm) bản word chuẩn kiến thức, trình bày đẹp mắt, dễ dàng chỉnh sửa:
- B1: Gửi phí vào tk:
1133836868- CT TNHH DAU TU VA DV GD VIETJACK - Ngân hàng MB (QR) - B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận giáo án
I. MỤC TIÊU
1. Về kiến thức
– Mô tả, nhắc lại được được công thức xác suất toàn phần và công thức Bayes.
– Hiểu được bảng số liệu 2 x 2 và biết tính xác suất dựa trên bảng số liệu 2 x 2 và sơ đồ cây.
– Sử dụng được công thức xác suất toàn phần và công thức Bayes để tính xác suất có điều kiện và giải quyết một số bài toán thực tế.
– Sử dụng được sơ đồ cây để tính xác suất có điều kiện và giải quyết một số bài toán thực tế.
2. Về năng lực
2.1. Năng lực chung:
– Tự chủ và tự học: HS tự chuẩn bị bài ở nhà, trả lời được những câu hỏi ở HĐKP.
– Giao tiếp và hợp tác: HS hoạt động nhóm thông qua việc tính xác suất có sử dụng công thức xác suất toàn phần và công thức Bayes.
2.2. Năng lực Toán học:
– Giải quyết vấn đề toán học: Giải quyết bài toán toán thực tế “mỗi liên hệ giữa điện thoại di động và tai nạn giao thông” thông qua công thức xác suất toàn phần và công thức Bayes.
– Tư duy và lập luận toán học: sử dụng công thức xác suất toàn phần và công thức Bayes để tính xác suất có điều kiện trong HĐTH 1, 2 và HĐVD.
3. Về phẩm chất
– Chăm chỉ: Có chuẩn bị bài trước ở nhà, chuẩn bị các kiến thức liên quan đến xác suất toàn phần, công thức Bayes và tham gia tốt hoạt động nhóm.
– Trung thực: HS thừa nhận và học tập các kết quả đúng của các bạn thông qua các hoạt động giải các bài tập luyện tập, thực hành, vận dụng.
II. THIẾT BỊ DẠY HỌC VÀ HỌC LIỆU
1. Đối với giáo viên: Kế hoạch dạy học, SGK, SGV, ti vi, bài trình chiếu.
2. Đối với học sinh: SGK, máy tính cầm tay, đồ dùng học tập.
III. TIẾN TRÌNH DẠY HỌC
A. KHỞI ĐỘNG
Hoạt động: Khởi động
a) Mục tiêu: Gợi mở, kết nối HS với bài Công thức xác suất toàn phần và công thức Bayes thông qua bài toán thực tế về xét nghiệm SAR–CoV–2.
b) Nội dung: GV yêu cầu HS đọc đề và yêu cầu của HĐKĐ và trả lời câu hỏi làm sao biết khả năng người đó thực sự nhiễm virus là cao hay thấp?
c) Sản phẩm: HS trả lời được câu hỏi: đề biết khả năng người đó thực sự nhiễm virus là cao hay thấp cần tính xác suất nhiễm bệnh khi bị kết quả dương tính.
d) Tổ chức thực hiện:
* GV chuyển giao nhiệm vụ học tập: Mỗi HS đọc đề và thực hiện yêu cầu của HĐKĐ.
* HS thực hiện nhiệm vụ học tập: HS suy nghĩ tìm ra câu trả lời.
* Báo cáo kết quả hoạt động và thảo luận: HS xung phong phát biểu ý kiến, quan điểm cá nhân.
* Kết luận nhận định: HS làm tốt yêu cầu của GV (chưa kết luận đúng sai).
B. KHÁM PHÁ – THỰC HÀNH – VẬN DỤNG
1. Công thức xác suất toàn phần
Hoạt động 1.1: Khám phá
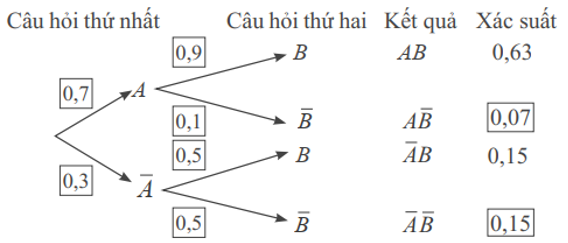
a) Mục tiêu: Nhắc lại cho HS về sơ đồ cây, liên kết với công thức xác suất toàn phần.
b) Nội dung: GV yêu cầu HS thực hiện HĐKP 1, hoàn thành sơ đồ cây.
c) Sản phẩm:
d) Tổ chức thực hiện:
* GV chuyển giao nhiệm vụ học tập: GV yêu cầu HS quan sát sơ đồ cây, đọc đề và điền các giá trị thích hợp vào dấu .
* HS thực hiện nhiệm vụ học tập: HS thực hiện bài tập cá nhân, đọc đề và điền giá trị thích hợp vào .
* Báo cáo kết quả hoạt động và thảo luận: HS xung phong điền giá trị thích hợp vào sơ đồ cây. HS khác nhận xét, đặt câu hỏi.
* Kết luận nhận định:
- GV yêu cầu HS nêu ý nghĩa của biến cố và . Ta thấy biến cố B là hợp của hai biến cố xung khắc và . Do đó:
- GV gọi HS đọc KTTT và phần Chú ý.
Hoạt động 1.2: Thực hành
a) Mục tiêu: HS thực hành sử dụng công thức xác suất toàn phần để tính xác suất của biến cố.
b) Nội dung: HS tính xác suất tắc đường trong HĐTH 1.
c) Sản phẩm: Gọi A là biến cố “Buổi sáng bị tắc đường” và B là biến cố “Buổi sáng trời mưa”
Do xác suất tắc đường khi trời mưa là 0,7 nên
Do xác suất tắc đường khi trời không mưa là 0,2 nên
Do xác suất trời mưa vào buổi sáng là 0,1 nên ; xác suất trời không mưa là
Áp dụng công thức xác suất toàn phần, ta có xác suất bị tắc đường là
d) Tổ chức thực hiện:
* GV chuyển giao nhiệm vụ học tập: GV yêu cầu HS làm việc theo nhóm 4 HS. HS đọc HĐTH 1 và suy nghĩ cách làm bài, sau đó ghi ra phiếu học tập, chuẩn bị lên bảng trình bày.
* HS thực hiện nhiệm vụ học tập: HS đọc HĐTH , trình bày chi tiết vào phiếu học tập.
* Báo cáo kết quả hoạt động và thảo luận: GV gọi nhóm, đại diện nhóm lên bảng trình bày. Các HS khác đối chiếu, nhận xét bài làm của nhóm mình sau đó đóng góp ý kiến.
* Kết luận nhận định: HS luyện tập được kĩ năng tính xác xuất của một biến cố bằng công thức xác suất toàn phần.
2. Công thức Bayes
Hoạt động 2.1: Khám phá
a) Mục tiêu: Hiểu được bảng dữ liệu thống kê 2 x 2; tính được xác suất có điều kiện dựa trên bảng dữ liệu thống kê 2 x 2.
b) Nội dung: HS đọc bảng số liệu và tính xác suất có điều kiện.
c) Sản phẩm: Gọi A là biến cố “Học sinh được chọn bị tật khúc xạ” và B là biến cố “Học sinh được chọn là nam”.
a) Có 12 + 18 = 30 bạn bị tật khúc xạ. Trong đó có 18 bạn nam.
Do đó, xác suất bạn được chọn là nam khi biết bạn đó bị tật khúc xạ là:
b) Có 18 + 32 = 50 bạn nam. Trong đó có 18 bạn bị tật khúc xạ.
Do đó, xác suất bạn được chọn bị tật khúc xạ khi biết bạn đó là nam là:
d) Tổ chức thực hiện:
* GV chuyển giao nhiệm vụ học tập: GV cho học sinh đọc bảng dữ liệu và yêu cầu HS làm việc theo nhóm 4 HS. Các nhóm chẵn trả lời câu a, các nhóm lẻ trả lời câu b điền vào phiếu học tập.
* HS thực hiện nhiệm vụ học tập: Các nhóm HS quan sát bảng và trả lời câu hỏi được giao trong HĐKP 2.
* Báo cáo kết quả hoạt động và thảo luận: GV chọn 2 nhóm, một nhóm chẵn, một nhóm lẻ. Nhóm HS được chọn cử đại diện lên bảng để trình bày kết quả của nhóm. Các nhóm khác ghi chép, đối chiếu, góp ý, nhận xét.
* Kết luận nhận định: HS tính được xác suất và hiểu bảng dữ liệu 2 x 2.
– GV dẫn dắt HS xây dựng công thức Bayes.
– GV gọi HS đọc KTTT của công thức Bayes và phần Chú ý
– GV hướng dẫn HS tìm hiểu Ví dụ 2.
– GV hướng dẫn HS tìm hiểu Ví dụ 3.
Hoạt động 2.2: Thực hành
a) Mục tiêu: HS thực hành sử dụng công thức Bayes để tính xác suất có điều kiện.
b) Nội dung: HS tính xác suất “vật thể bay là mục tiêu thật khi radar phát tín hiệu cảnh báo” trong HĐTH 2.
c) Sản phẩm: Xác suất vật thể bay là mục tiêu thật là:
d) Tổ chức thực hiện:
* GV chuyển giao nhiệm vụ học tập: GV yêu cầu HS làm việc theo nhóm, hoàn thành phiếu học tập.
* HS thực hiện nhiệm vụ học tập: HS làm việc theo nhóm: trao đổi để trả lời câu hỏi xác suất vật thể bay là mục tiêu thật khi radar phát tín hiệu.
* Báo cáo kết quả hoạt động và thảo luận: GV chọn một nhóm trình bày kết quả. Các nhóm khác đối chiếu kết quả trên bảng với bài làm của nhóm mình. Nhận xét, đặt câu hỏi và góp ý.
* Kết luận nhận định: HS giải quyết được bài toán, tính đúng xác suất có điều kiện.
Hoạt động 2.3: Vận dụng
a) Mục tiêu: Vận dụng công thức xác suất toàn phần và công thức Bayes để trả lời được câu hỏi “sử dụng điện thoại di động khi lái xe làm tăng xác suất gây tai nạn lên bao nhiêu lần?”.
b) Nội dung: HS trả lời câu hỏi trong HĐVD.
c) Sản phẩm: HS trả lời:
Việc sử dụng điện thoại di động khi lái xe làm tăng xác suất gây tai nạn lên 5 lần.
................................
................................
................................
(Nguồn: NXB Giáo dục)
Trên đây tóm tắt một số nội dung miễn phí trong bộ Giáo án Toán 12 Chân trời sáng tạo năm 2024 mới nhất, để mua tài liệu đầy đủ, Thầy/Cô vui lòng xem thử: