Giáo án Toán 12 Bài 3: Lôgarit

❮ Bài trước Bài sau ❯

Giáo án Toán 12 Bài 3: Lôgarit

Xem thử

Chỉ 250k mua trọn bộ Giáo án Toán 12 bản word có lời giải chi tiết:

B1: gửi phí vào tk: 0712000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)
B2: Nhắn tin tới Zalo VietJack Official - nhấn vào đây để thông báo và nhận giáo án

I. Mục tiêu

1. Về kiến thức

- Biết khái niệm lôgarit cơ số a (a>0, a $\neq$ 1) của một số dương.

- Biết các tính chất của lôgarit (so sánh hai logarit cùng cơ số, quy tắc tính lôgarit, đổi cơ số của lôgarit).

- Biết khái niệm lôgarit thập phân và lôgarit tự nhiên.

2. Về năng lực

2.1. Năng lực chung

- Năng lực giao tiếp: Học sinh chủ động tham gia và trao đổi thông qua hoạt động nhóm.

- Năng lực hợp tác: Học sinh biết phối hợp, chia sẻ trong các hoạt động tập thể.

2.2. Năng lực toán học

- Năng lực giải quyết vấn đề: Biết vận dụng định nghĩa để tính một số biểu thức chứa lôgarit đơn giản. Biết vận dụng tính chất của lôgarit vào các bài tập biến đổi, tính toán các biểu thức chứa lôgarit.

- Năng lực sử dụng công cụ và phương tiện toán học: HS biết Sử dụng máy tính cầm tay tính logarit.

3.Phẩm chất

- Nghiêm túc, tích cực, chủ động, độc lập và hợp tác trong hoạt động nhóm.

- Say sưa, hứng thú trong học tập và tìm tòi nghiên cứu liên hệ thực tiễn.

- Chủ động phát hiện, chiếm lĩnh tri thức mới, biết quy lạ về quen, có tinh thần hợp tác xây dựng cao.

II. Thiết bị dạy học và học liệu

+ Giáo án, phiếu học tập, phấn, thước kẻ, máy chiếu, ...

+ Link video khởi động

(Nguồn: http://ed.ted.com/lessons/how-does-math-guide-our-ships-at-sea-george-christoph)

III. Tiến trình dạy học

Hoạt động 1: Hoạt động khởi động 1.

Hoạt động 1.1: HS xem video để thấy được ứng dụng của toán học trong thực tiễn.

a. Mục tiêu: Tạo sự thích thú, khơi gợi trí tò mò cho học sinh về kiến thức của bài mới.

b. Nội dung:

Giới thiệu chung về chủ đề: Khái niệm Lôgarit là tri thứctoán học được phát sinh từ nhu cầu tính toán và ứng dụng nhiều trong thực tiễn. Khi xuất hiện đầu tiên trong lịch sử, Lôgarit cũng đã khẳng định vị thế riêng. Nhà Toán học Pháp, Pierr S.Laplace (1749-1827) đã nói rằng: “Việc phát minh ra Lôgarit đã kéo dài tuổi thọ của các nhà tính toán”. Với tầm quan trọng được thừa nhận, Lôgarit được đưa vào giảng dạy trong chương trình toán Phổ thông. Lôgarit là đối tượng chiếm vị trí và vai trò quan trọng trong chương trình toán phổ thông. Trong chủ đề này chúng ta sẽ tìm hiểu rõ hơn về vai trò và các ứng dụng thực tiễn đó.

GV mở video How does math guide our ships at sea? - George Christoph (Toán học giúp các tàu của chúng ta định vị trên biển như thế nào?). Thời lượng: 4 phút 38 giây.

(Nguồn:http://ed.ted.com/lessons/how-does-math-guide-our-ships-at-sea-george-christoph)

Câu hỏi thảo luận: Ba phát minh nào giúp cho việc định vị trên biển trở nên dễ dàng hơn?

Trong đó, phát minh nào được đánh giá là có tầm quan trọng hơn cả.

Vậy các phép tính logarit là gì ? Chúng ta hãy cùng tìm hiểu chúng trong bài học ngày hôm nay.

c. Sản phẩm:

- HS xem video và hiểu được ý nghĩa của toán học trong đời sống

- HS trả lời được câu hỏi: Ba phát minh: Kính lục phân, Đồng hồ, và các phép tính Logarit.

Phát minh quan trọng hơn cả: Các phép tính Logarit.

d. Cách thức tổ chức:

- GV mở video và yêu cầu cả lớp xem

- Sau khi xem video HS hoạt động nhóm 4HS trả lời các câu hỏi thảo luận

Hoạt động 1.2: HS tham gia trò chơi “Nhanh như chớp”.

a. Mục tiêu: Thay đổi không khí và tạo hứng thú khi HS thấy được kiến thức logarit rất gần gũi.

b. Nội dung: HS trả lời câu hỏi

Giáo án Toán 12 Bài 3: Lôgarit | Giáo án Giải tích 12

Câu hỏi thảo luận:

Có số x, y nào để 2^x = 0 và 3^y = -1không? Từ đó nhận xét dấu của $a^{α}$ với a>0, a $\neq$ 1?

c. Sản phẩm:

- HS trả lời được các câu hỏi

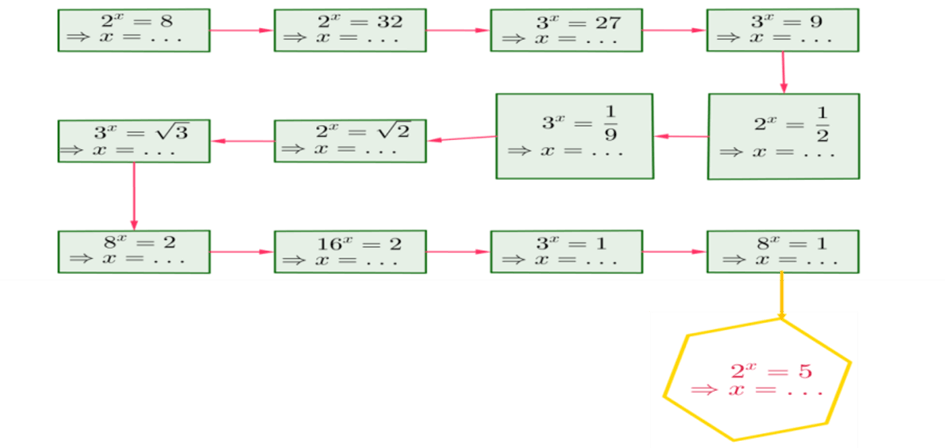
- HS số ô số 13 có câu hỏi 2^x = 5sẽ không đưa ra được câu trả lời cụ thể như các bạn.

- Không tồn tại số x, y thỏa mãn các yêu cầu trên và $a^{α}$ >0, $\forall α$ .

d. Cách thức tổ chức:

- Giáo viên chuẩn bị một slide như ví dụ dưới đây. Trong slide các ô sẽ được hiện ra lần lượt theo sự điều khiển của giáo viên. Giáo viên gọi nhanh từng học sinh trả lời. Thời gian cho mỗi câu là 3s. Nếu HS được hỏi chưa có câu trả lời thì phải chuyển ngay sang học sinh khác.

- HS số ô số 13 có câu hỏi 2^x = 5sẽ không đưa ra được câu trả lời cụ thể như các bạn thì GV trả lời: số x có tồn tại và xđược kí hiệu là log₂5, đọc là logarit cơ số 2 của 5.

- Tiếp đến câu hỏi thảo luận

2. Hoạt động 2: Hình thành kiến thức mới

I. Khái niệm Lôgarit

HĐ1. Định nghĩa

a) Mục tiêu: Hình thành định nghĩa lôgarit và tính lôgarit bằng định nghĩa.

b) Nội dung: GV yêu HS cầu đọc SGK và trả lời câu hỏi

H1: Cho hai số dương a, b với a $\neq$ 1. Số thực $α$ được gọi là lôgarit cơ số a của b khi nào?

H2: Ví dụ 1: Tính $\log_{\frac{1}{2}} 8$

H3: Ví dụ 2: Tính $\log_{3} \frac{1}{27}$

H4: Có tồn tại lôgarit của số âm và số 0 không? Vì sao?

c) Sản phẩm:

1. Định nghĩa

Cho hai số dương a, b với a $\neq$ 1 . Số thực $α$ thỏa mãn đẳng thức $a^{α}$ =b được gọi là lôgarit cơ số a của b và kí hiệu là log_ab.

Suy ra: $α$ = log_ab $\Leftrightarrow$ $a^{α}$ =b

Ví dụ 1: Ta có $\log_{\frac{1}{2}} 8$ = -3 vì ${(\frac{1}{2})}^{- 3}$ = 8

Ví dụ 2: Ta có $\log_{3} \frac{1}{27}$ = -3 vì 3^-3 = $\frac{1}{27}$

Chú ý: Không có lôgarit của số âm và số 0.

d) Tổ chức thực hiện

*Chuyển giao*	- Gv đặt vấn đề: hai số dương a, b với a $\neq$ 1 luôn tồn tại duy nhất một số thực $α$ sao cho $a^{α}$ = b. Số thực $α$ đó được gọi là lôgarit cơ số a của b . Từ đó yêu cầu học sinh trả lời câu hỏi H1. - Gv ghi Ví dụ 1, Ví dụ 2 lên bảng để cả lớp theo dõi và thực hiện. - Gv nêu câu hỏi H4.
*Thực hiện*	- HS thảo luận cặp đôi thực hiện nhiệm vụ. - GV theo dõi, hỗ trợ, hướng dẫn các nhóm.
*Báo cáo thảo luận*	- Các cặp thảo luận đưa ra định nghĩa lôgarit. - Thực hiện được VD1,2 và viết câu trả lời vào bảng phụ. - Thuyết trình các bước thực hiện. - Các nhóm khác nhận xét hoàn thành sản phẩm. Chú ý: Học sinh phải nêu bật được: $α = \log_{a} b \Leftrightarrow a^{α} = b$ Không có lôgarit của số âm và số 0
*Đánh giá, nhận xét, tổng hợp*	- GV nhận xét thái độ làm việc, phương án trả lời của học sinh, ghi nhận và tuyên dương học sinh có câu trả lời tốt nhất. Động viên các học sinh còn lại tích cực, cố gắng hơn trong các hoạt động học tiếp theo - Chốt định nghĩa lôgarit.

................................

Trên đây tóm tắt một số nội dung có trong bộ Giáo án Toán 12 năm 2023 mới nhất, để mua tài liệu đầy đủ, Thầy/Cô vui lòng truy cập Tài liệu Giáo án, đề thi mới, chuẩn

Xem thử

Xem thêm các bài soạn Giáo án Toán lớp 12 mới nhất, hay khác:

❮ Bài trước Bài sau ❯