Giáo án Toán 9 Bài 1: Hàm số y = ax (a ≠ 0) mới nhất
Giáo án Toán 9 Bài 1: Hàm số y = ax (a ≠ 0) mới nhất
I. Mục tiêu:
Qua bài này HS cần:
1. Kiến thức:
- Thấy được trong thực tế có những hàm số dạng y=ax2(a 0).
- Phát biểu được tính chất của hàm số y=ax2(a 0).
- Liên hệ được ví dụ và ứng dụng thực tế của hàm.
2. Kĩ năng:
- Biết cách tính giá trị của hàm số tương ứng với giá trị cho trước của biến số.
- Tính được giá trị của hàm số tương ứng với giá trị cho trước của biến số.
3. Thái độ:
- Nghiêm túc và hứng thú học tập.
4. Định hướng năng lực, phẩm chất
- Năng lực tính toán, giải quyết vấn đề, hợp tác, giao tiếp, tự học.
Phẩm chất: Tự tin, tự chủ
II. Chuẩn bị:
- Gv : Phấn mầu, bảng phụ, thước thẳng
- Hs: Đồ dùng học tập, đọc trước bài.
III. Tiến trình dạy học:
1. Ổn định :(1 phút)
2. Bài mới :
| Giáo viên | Học sinh | Nội dung ghi bài | ||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Hoạt động 1: KHỞI ĐỘNG – 1p Như sách giáo khoa đặt vấn đề: giới thiệu về chương IV. HS thấy được sự cần thiết và tính tò mò phải đi tìm hiểu về một hàm số mới dạng y = ax2 (a ≠ 0) khác với hàm số bậc nhất một ẩn y = ax + b (a ≠ 0) đã được học. |
||||||||||||||||||||||||||||||||||
|
Hoạt động 2: HÌNH THÀNH KIẾN THỨC – 29p GV Tổ chức các HĐ để HS định hướng phát triển năng lực và phẩm chất cần có trong lúc hình thành được 3 đơn vị kiến thức mới: Công thức TQ hàm số y = ax2 (a ≠ 0); tính chất và nhận xét. Ví dụ mở đầu Mục tiêu: HS phát biểu được ví dụ mở đầu trong sgk, chỉ ra được sự tương ứng 1-1 giữa t và s, qua đó phát biểu được khái niệm hàm số y = ax2 (a ≠ 0) Kĩ thuật sử dụng: Động não, hoàn tất một nhiệm vụ, |
||||||||||||||||||||||||||||||||||
GV gọi một HS đọc ví dụ mở đầu. GV: Trong thực tế còn rất nhiều cặp đại lượng cũng được liên hệ với nhau bởi công thức có dạng y = ax2 (a ≠ 0), chẳng hạn diện tích hình vuông và cạnh của nó: S = a2, diện tích hình tròn và bán kính của nó S = πR2… GV: Hàm số y = ax2 (a ≠ 0) là dạng đơn giản nhất của hàm số bậc hai. Sau đây chúng ta xét các tính chất của hàm số đó. |
HS: Đọc bài HS quan sát trả lời HS trả lời HS nắm chắc công thức tổng quát của hàm số y = ax2 (a ≠ 0) |
1. Ví dụ mở đầu Xem SGK/28 |
||||||||||||||||||||||||||||||||
|
GV HD HS quan sát các bảng giá trị của hai hàm số cụ thể a > 0 ; a < 0 qua đó rút ra nhận xét và tổng quát nên thành tính chất của hàm số mới vừa học. 2/ Tính chất của hàm số y = ax2 (a ≠ 0) Bảng 1:
Bảng 2:
|
||||||||||||||||||||||||||||||||||
GV: Gọi HS nhận xét bài làm của các bạn. GV: Chỉ vào bảng số 1 và nêu câu hỏi của bài ?2 sgk. GV: Yêu cầu HS nhận xét tương tự đối với hàm số y = –2x2. GV: Nói một cách tổng quát, hàm số y = ax2 (a ≠ 0) xác định với mọi giá trị của x thuộc R và người ta chứng minh được nó có các tính chất sau: (GV đưa lên bảng phụ các tính chất của hàm số đó). |
HS nhận xét bài làm của các bạn. HS trả lời hai câu hỏi trong bài tập ?2 sgk. HS nhận xét tương tự đối với hàm số y = –2x2. |
*Đối với hàm số: y = 2x2 - Khi x<0; x tăng thì y giảm - Khi x>0; x tăng thì y tăng *Đối với hàm số: y = -2x2 - Khi x<0; x tăng thì y tăng - Khi x>0; x tăng thì y giảm * Tổng quát: - Nếu a>0 thì hàm số ĐB khi x>0; NB khi x<0 - Nếu a<0 thì hàm số ĐB khi x<0; NB khi x>0 |
||||||||||||||||||||||||||||||||
| GV yêu cầu HS hoạt động nhóm làm bài ?3 và cự đại diện một nhóm lên bảng trình bày bài làm. GV nêu phần nhận xét SGK |
HS nghe GV nêu tổng quát. HS đọc kết luận tổng quát. . . HS hoạt động nhóm làm bài ?3 và cử đại diện một nhóm lên bảng trình bày bài làm.s HS đại diện hai nhóm lên bảng điền vào ô trống |
?3: Đối với hàm số y=2x2, khi x 0 giá trị của y dương, khi x=0 thì y=0 Đối với hàm số y=2x2, khi x 0 giá trị của y âm, khi x=0 thì y=0 * Nhận xét: Với y = ax2 (a 0) - Nếu a>0 thì y>0 với mọi x ≠ 0; y=0 khi x=0. Giá trị nhỏ nhất của hàm số là y = 0 - Nếu a<0 thì y>0 với mọi x ≠ 0; y=0 khi x=0 thì giá trị lớn nhất của hàm số là y = 0 |
||||||||||||||||||||||||||||||||
|
Hoạt động 3, 4: LUYỆN TẬP, VẬN DỤNG – 8p Mục tiêu: Nhắc lại được tính chất của hàm số y = ax2 ( a 0 ), vận dụng kiến thức giải bài tập có liên quan. Kĩ thuật sử dụng: Hỏi và trả lời, hoàn tất một nhiệm vụ. Cho HS làm ?4/30 để củng cố lại tính chất và nhận xét trên GV đưa bảng phụ lên, yêu cầu hai HS đại diện hai nhóm lên bảng điền vào ô trống
HS1: Nhận xét: a = y = 0 khi x = 0. Giá trị nhỏ nhất của hàm số là y = 0. HS2: Nhận xét : a = – y = 0 khi x = 0. Giá trị lớn nhất của hàm số là y = 0. |
||||||||||||||||||||||||||||||||||
Hoạt động 5: TÌM TÒI, MỞ RỘNG – 6p Mục tiêu: Biết sử dụng máy tính để tính GTBT PP: Thực hành 1. Dùng máy tính CASIO để tính giá trị của một biểu thức • Ví dụ 1: Tính giá trị của biểu thức : A = 3x2 – 3,5x + 2 với x = 4,13 HS thực hiện tính bằng máy CASIO như SGK, tr32 • Ví dụ 2: Tính diện tích của một hình tròn có bkính R ( S = πR2 ) với R = 0,61; 1,53 ; 2,49 HS thực hiện tính bằng máy CASIO như SGK, tr32 2. Bài tập về nhà: số 2; 3 tr 31 SGK ; bài 1 , 2 tr 36 SBT. - GV: Hướng dẫn bài 3 SGK : Công thức F = av2 a) Tính a v = 2 m/s ; F = 120 N ; F = av2 => a = b) Tính F v1 = 10 m/s ; v2 = 20 m/s ; F = av2 |
||||||||||||||||||||||||||||||||||



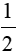 > 0 nên y > 0 với mọi x ≠ 0;
> 0 nên y > 0 với mọi x ≠ 0;