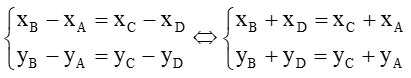Trong mặt phẳng tọa độ Oxy, cho tứ giác ABCD có A(xA; yA); B(xB; yB); C(xC; yC); D(xD; yD)

Trong mặt phẳng tọa độ Oxy, cho tứ giác ABCD có A(x; y); B(x; y); C(x; y); D(x; y). Chứng minh rằng tứ giác ABCD là hình bình hành khi và chỉ khi x + x = x + x và y + y = y + y

Giải sách bài tập Toán 10 Bài 1: Tọa độ của vectơ

Bài 10 trang 62 SBT Toán 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho tứ giác ABCD có A(x_A; y_A); B(x_B; y_B); C(x_C; y_C); D(x_D; y_D). Chứng minh rằng tứ giác ABCD là hình bình hành khi và chỉ khi x_A + x_C = x_B + x_D và y_A + y_C = y_B + y_D

Lời giải:

Ta có: $\overrightarrow{AB}$= (x_B - x_A; y_B - y_A), $\overrightarrow{DC}$= (x_C - x_D;y_C - y_D)

Do ABCD là hình bình hành nên ta có: $\overrightarrow{AB}$=$\overrightarrow{DC}$

Hay

Vậy bài toán được chứng minh.