Lập bảng xét dấu với mỗi tam thức bậc hai sau trang 52 sách bài tập Toán 10

Lập bảng xét dấu với mỗi tam thức bậc hai sau:

Giải sách bài tập Toán 10 Bài 3: Dấu của tam thức bậc hai

Bài 23 trang 52 SBT Toán 10 Tập 1: Lập bảng xét dấu với mỗi tam thức bậc hai sau:

a) f(x) = 3x² – 7x + 4;

b) f(x) = 25x² + 10x + 1;

c) f(x) = 3x² – 2x + 8;

d) f(x) = – 2x² + x + 3;

e) f(x) = – 3x² + 6x – 3;

f) f(x) = – 5x² + 2x – 4.

Lời giải:

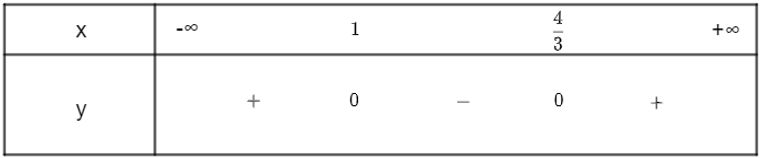
a) Xét tam thức bậc hai f(x) = 3x² – 7x + 4 , có a = 3 > 0 và ∆ = (– 7)² – 4.3.4 = 1 > 0.

Suy ra tam thức có hai nghiệm phân biệt x = 1 và x = $\frac{4}{3}$.

Khi đó ta có bảng xét dấu sau: 

b) Xét tam thức bậc hai f(x) = 25x² + 10x + 1, có a = 25 > 0 và ∆ = 10² – 4.25.1 = 0.

Suy ra tam thức có nghiệm kép x = $-\frac{1}{5}$.

Khi đó ta có bảng xét dấu sau:

c) Xét tam thức bậc hai f(x) = 3x² – 2x + 8, có a = 3 > 0 và ∆ = (– 2)² – 4.3.8 = – 92 < 0.

Suy ra tam thức vô nghiệm.

Khi đó ta có bảng xét dấu sau:

d) Xét tam thức bậc hai f(x) = – 2x² + x + 3, có a = – 2 < 0 và ∆ = 1² – 4.(– 2).3 = 25 > 0.

Suy ra tam thức có hai nghiệm phân biệt x = – 1 và x = $\frac{3}{2}$.

Khi đó ta có bảng xét dấu sau:

e) Xét tam thức bậc hai f(x) = – 3x² + 6x – 3, có a = – 3 < 0 và ∆ = 6² – 4.(– 3).(– 3) = 0.

Suy ra tam thức có nghiệm kép x = 1.

Khi đó ta có bảng xét dấu sau:

f) Xét tam thức bậc hai f(x) = – 5x² + 2x – 4, có a = – 5 < 0 và ∆ = 2² – 4.(– 5).(– 4) = – 76 < 0.

Suy ra tam thức vô nghiệm

Khi đó ta có bảng xét dấu sau: