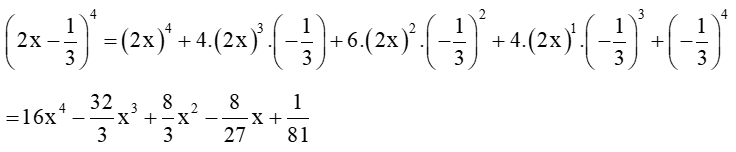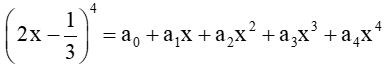Cho (2x-1/3)^4 = (a0)x + (a1)x + (a2)x^2 + (a3)x^3 + (a4)x^4. Tính

Cho . Tính:

Giải sách bài tập Toán 10 Bài 4: Nhị thức Newton

Bài 35 trang 16 SBT Toán 10 Tập 2: Cho 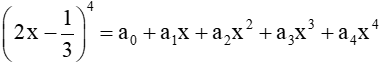Cho (2x-1/3)^4 = (a0)x + (a1)x + (a2)x^2 + (a3)x^3 + (a4)x^4. Tính . Tính:

a) a₂;

b) a₀ + a₁ + a₂ + a₃ + a₄.

Lời giải:

a) Ta có:

Cho (2x-1/3)^4 = (a0)x + (a1)x + (a2)x^2 + (a3)x^3 + (a4)x^4. Tính

Ta thấy a₂ là hệ số của x².

Số hạng chứa x² trong khai triển biểu thức ${(2 x - \frac{1}{3})}^{4}$ là $\frac{8}{3} x^{2}$ .

Suy ra hệ số của x² trong khai triển biểu thức ${(2 x - \frac{1}{3})}^{4}$ là $\frac{8}{3}$ .

Tức là, $a_{2} = \frac{8}{3}$ .

b) Ta có Cho (2x-1/3)^4 = (a0)x + (a1)x + (a2)x^2 + (a3)x^3 + (a4)x^4. Tính

Chọn x = 1, ta được:

${(2.1 - \frac{1}{3})}^{4}$ = a₀ + a₁ + a₂ + a₃ + a₄ = a₀ + a₁.1 + a₂.1² + a₃.1³ + a₄.1⁴

⇔ $\frac{625}{81}$ = a₀ + a₁ + a₂ + a₃ + a₄.

Vậy a₀ + a₁ + a₂ + a₃ + a₄ = $\frac{625}{81}$ .