Vẽ đồ thị của mỗi hàm số sau: a) y = 2x^2 – 8x + 1; b) y = – x^2 + 4x – 3

Giải sách bài tập Toán 10 Bài tập cuối chương 3 trang 61, 62, 63

Bài 50 trang 62 SBT Toán 10 Tập 1: Vẽ đồ thị của mỗi hàm số sau:

a) y = 2x² – 8x + 1;

b) y = – x² + 4x – 3.

Lời giải:

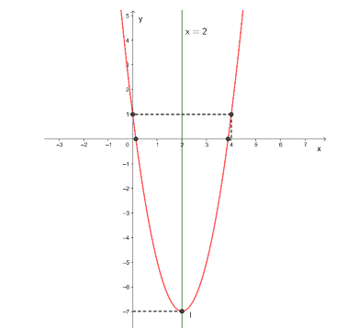
a) Xét hàm số y = 2x² – 8x + 1, có a = 2 > 0, ∆ = (– 8)² – 4.1.2 = 56 > 0.

- Điểm đỉnh: I = $\left(-\frac{b}{2a};-\frac{∆}{4a}\right)=\left(-\frac{-8}{2.2};\frac{56}{4.2}\right)=\left(2,-7\right)$.

- Trục đối xứng là x = 2.

- Vì a = 2 > 0 thì đồ thị hàm số có bề lõm hướng lên trên.

- Đồ thị hàm số cắt trục tung tại điểm có tọa độ (0; 1).

- Điểm đối xứng với điểm (0; 1) qua trục đối xứng là (4; 1).

- Đồ thị cắt trục hoành tại hai điểm có tọa độ $\left(\frac{4-\sqrt{14}}{2},0\right)$ và $\left(\frac{4+\sqrt{14}}{2};0\right)$

Ta có hình vẽ sau:

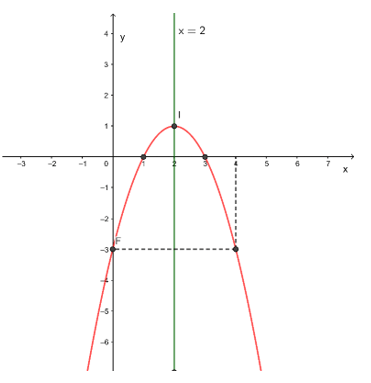
b) Xét hàm số y = – x² + 4x – 3, có a = – 1 < 0, ∆ = 4² – 4.(–1).(–3) = 4 > 0.

- Điểm đỉnh: I = $(-\frac{b}{2a},-\frac{∆}{4a})=\left(-\frac{4}{2.\left(-1\right)};-\frac{4}{4\left(-1\right)}\right)=\left(2;1\right)$.

- Trục đối xứng là x = 2.

- Vì a = – 1 < 0 thì đồ thị hàm số có bề lõm hướng xuống dưới.

- Đồ thị hàm số cắt trục tung tại điểm có tọa độ (0; – 3).

- Điểm đối xứng với điểm (0; – 3) qua trục đối xứng là (4; – 3).

- Đồ thị cắt trục hoành tại hai điểm có tọa độ (1; 0) và (3; 0)

Ta có hình vẽ sau: