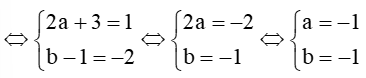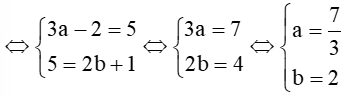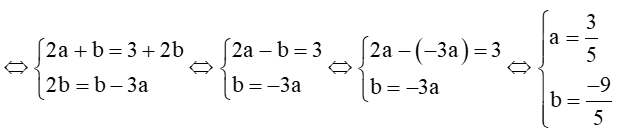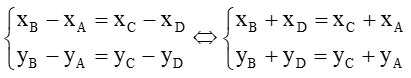Giải SBT Toán 10 trang 62 Tập 2 Cánh diều

❮ Bài trước Bài sau ❯

Haylamdo biên soạn giải Sách bài tập Toán 10 trang 62 Tập 2 trong Bài 1: Tọa độ của vectơ SBT Toán 10 Cánh diều Tập 2 hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 10 trang 62.

Giải SBT Toán 10 trang 62 Tập 2 Cánh diều

Bài 8 trang 62 SBT Toán 10 Tập 2: Tìm các số thực a và b sao cho mỗi cặp vectơ sau bằng nhau:

a) $\vec{m}$ = (2a+3;b-1) và $\vec{n}$ = (1;-2);

b) $\vec{u}$ = (3a-2;5) và $\vec{v}$ = (5;2b+1);

c) $\vec{x}$ = (2a+b;2b) và $\vec{y}$ = (3+2b;b-3a).

Lời giải:

2 vectơ bằng nhau thì tọa độ tương ứng của chúng phải bằng nhau.

a) Ta có: $\vec{m}$ = (2a+3;b-1) và $\vec{n}$ = (1;-2) bằng nhau

Tìm các số thực a và b sao cho mỗi cặp vectơ sau bằng nhau

Vậy a = – 1, b = – 1.

b. Ta có: $\vec{u}$ = (3a-2;5) và $\vec{v}$ = (5;2b+1) bằng nhau

Tìm các số thực a và b sao cho mỗi cặp vectơ sau bằng nhau

Vậy a = $\frac{7}{3}$ , b = 2.

c. Ta có: $\vec{x}$ = (2a+b;2b) và $\vec{y}$ = (3+2b;b-3a) bằng nhau

Tìm các số thực a và b sao cho mỗi cặp vectơ sau bằng nhau

Vậy a = $\frac{3}{5}$ và b = $\frac{- 9}{5}$ .

Bài 9 trang 62 SBT Toán 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho ba điểm không thẳng hàng A(- 4; 2), B(2; 4), C(8; - 2). Tìm tọa độ của điểm D sao cho tứ giác ABCD là hình bình hành.

Lời giải:

Ta có: $\vec{A B}$ = (2+4;4-2) = (6;2)

Gọi D(a; b) thì $\vec{D C}$ = (8-a;-2-b)

Do ABCD là hình bình hành nên ta có: $\vec{A B}$ = $\vec{D C}$

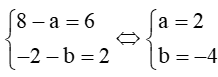
Hay Trong mặt phẳng tọa độ Oxy, cho ba điểm không thẳng hàng A(- 4; 2), B(2; 4), C(8; - 2) .

Suy ra D(2; -4).

Vậy D(2; -4).

Bài 10 trang 62 SBT Toán 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho tứ giác ABCD có A(x_A; y_A); B(x_B; y_B); C(x_C; y_C); D(x_D; y_D). Chứng minh rằng tứ giác ABCD là hình bình hành khi và chỉ khi x_A + x_C = x_B + x_D và y_A + y_C = y_B + y_D

Lời giải:

Ta có: $\vec{A B}$ = (x_B - x_A; y_B - y_A), $\vec{D C}$ = (x_C - x_D;y_C - y_D)

Do ABCD là hình bình hành nên ta có: $\vec{A B}$ = $\vec{D C}$

Hay Trong mặt phẳng tọa độ Oxy, cho tứ giác ABCD có A(xA; yA); B(xB; yB); C(xC; yC); D(xD; yD)

Vậy bài toán được chứng minh.

Bài 11 trang 62 SBT Toán 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho ba điểm không thẳng hàng M(1; - 2), N(3; 1), P(- 1; 2). Tìm tọa độ điểm Q sao cho tứ giác MNPQ là hình thang có MN // PQ và PQ = 2MN.

Lời giải:

Do tứ giác MNPQ là hình thang có MN // PQ

Nên $\vec{M N}$ cùng phương với $\vec{P Q}$ .

Mà PQ = 2MN, $\vec{M N}$ ngược hướng với $\vec{P Q}$

Suy ra $\vec{P Q}$ =-2. $\vec{M N}$ .

Gọi Q(a; b), ta có: $\vec{M N}$ =(3-1:1+2) và $\vec{P Q}$ =(a+1;b-2)

Trong mặt phẳng tọa độ Oxy, cho ba điểm không thẳng hàng M(1; - 2), N(3; 1), P(- 1; 2)