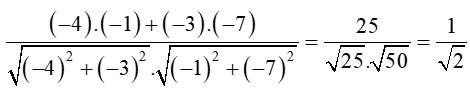Giải SBT Toán 10 trang 66 Tập 2 Cánh diều

---

Haylamdo biên soạn giải Sách bài tập Toán 10 trang 66 Tập 2 trong Bài 2: Biểu thức tọa độ của các phép toán vectơ SBT Toán 10 Cánh diều Tập 2 hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 10 trang 66.

Giải SBT Toán 10 trang 66 Tập 2 Cánh diều

Bài 12 trang 66 SBT Toán 10 Tập 2: Cho hai vectơ $\overrightarrow{u}$=(-1;3) và $\overrightarrow{v}$=(2;-5). Tọa độ của vectơ $\overrightarrow{u}$+$\overrightarrow{v}$ là:

A. (1; - 2);

B. (- 2; 1);

C. (- 3; 8);

D. (3; - 8).

Lời giải:

Ta có: $\overrightarrow{u}$+$\overrightarrow{v}$= ( -1 + 2; 3 + (-5)) = (1; -2).

Vậy chọn đáp án A.

Bài 13 trang 66 SBT Toán 10 Tập 2: Cho hai vectơ $\overrightarrow{u}$=(2;-3) và $\overrightarrow{v}$=(1;4). Tọa độ của vectơ $\overrightarrow{u}-2\overrightarrow{v}$ là:

A. (0; 11);

B. (0; - 11);

C. (- 11; 0);

D. (- 3; 10).

Lời giải:

Tọa độ của vectơ $\overrightarrow{u}-2\overrightarrow{v}$= (2-2.1;-3-2.4) = (0;-11)

Vậy chọn đáp án B.

Bài 14 trang 66 SBT Toán 10 Tập 2: Cho hai điểm A(4; - 1) và B(- 2; 5). Tọa độ trung điểm M của đoạn thẳng AB là:

A. (2; 4);

B. (- 3; 3);

C. (3; - 3);

D. (1; 2).

Lời giải:

Tọa độ trung điểm M của đoạn thẳng AB là:

x_M= $\frac{x_A+x_B}{2}=\frac{4+\left(-2\right)}{2}$=1

y_M= $\frac{y_A+y_B}{2}=\frac{-1+5}{2}$=2

Suy ra M(1; 2)

Vậy chọn đáp án D.

Bài 15 trang 66 SBT Toán 10 Tập 2: Cho tam giác ABC có A(4; 6), B(1; 2), C(7; - 2). Tọa độ trọng tâm G của tam giác ABC là:

A. $\left(4;\frac{10}{3}\right)$ ;

B. (8; 4);

C. (2; 4);

D. (4; 2).

Lời giải:

Tọa độ trọng tâm G của tam giác ABC là:

$x_G=\frac{x_A+x_B+x_C}{3}=\frac{4+1+7}{3}$=4

$y_G=\frac{y_A+y_B+y_C}{3}=\frac{6+2+\left(-2\right)}{3}$=2

Suy ra G(4; 2)

Vậy chọn đáp án D.

Bài 16 trang 66 SBT Toán 10 Tập 2: Cho hai điểm M(- 2; 4) và N(1; 2). Khoảng cách giữa hai điểm M và N là:

A. $\sqrt{13}$ ;

B. $\sqrt{5}$ ;

C. 13;

D. $\sqrt{37}$ .

Lời giải:

Khoảng cách giữa hai điểm M và N chính bằng độ dài vectơ $\overrightarrow{MN}$ và bằng

|$\overrightarrow{MN}$| = $\sqrt{{\left(x_N-x_M\right)}^2+{\left(y_N-y_M\right)}^2}=\sqrt{{\left(1+2\right)}^2+{\left(2-4\right)}^2}=\sqrt{13}$

Vậy chọn đáp án A.

Bài 17 trang 66 SBT Toán 10 Tập 2: Cho hai vectơ $\overrightarrow{u}$=(-4;-3) và $\overrightarrow{v}$=(-1;-7). Góc giữa hai vectơ $\overrightarrow{u}$ và $\overrightarrow{v}$ là:

A. 90⁰;

B. 60⁰;

C. 45⁰;

D. 30⁰.

Lời giải:

Ta có: cos($\overrightarrow{u}$;$\overrightarrow{v}$)

=

Suy ra ($\overrightarrow{u}$;$\overrightarrow{v}$)= ${45}^o$ .

Vậy chọn đáp án C.

Lời giải sách bài tập Toán lớp 10 Bài 2: Biểu thức tọa độ của các phép toán vectơ Cánh diều hay khác:

• Giải SBT Toán 10 trang 67 Tập 2