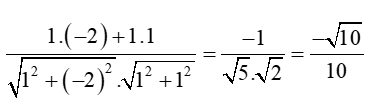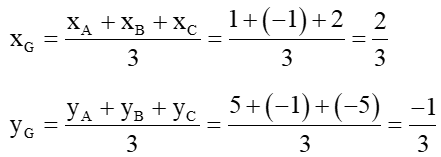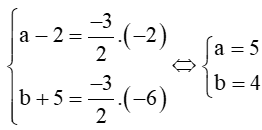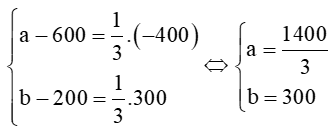Giải SBT Toán 10 trang 67 Tập 2 Cánh diều
Haylamdo biên soạn giải Sách bài tập Toán 10 trang 67 Tập 2 trong Bài 2: Biểu thức tọa độ của các phép toán vectơ SBT Toán 10 Cánh diều Tập 2 hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 10 trang 67.
Giải SBT Toán 10 trang 67 Tập 2 Cánh diều
Bài 18 trang 67 SBT Toán 10 Tập 2: Côsin của góc giữa hai vectơ =(1;1) và =(-2;1) là:
A. ;
B. ;
C. ;
D. .
Lời giải:
Côsin của góc giữa hai vectơ =(1;1) và =(-2;1) là:
cos(;)=
Vậy chọn đáp án C.
Bài 19 trang 67 SBT Toán 10 Tập 2: Cho tam giác ABC có A(2; 6), B(- 2; 2), C(8; 0). Khi đó, tam giác ABC là:
A. Tam giác đều;
B. Tam giác vuông tại A;
C. Tam giác có góc tù tại A;
D. Tam giác cân tại A.
Lời giải:
Ta có: =(-2-2;2-6) = (-4;-4) ⇒ AB = || =
=(8-2;0-6) = (6;-6) AC = ||= .
Ta lại có: .= (-4).6+(-4).(-6) = 0
Nên vuông góc với hay tam giác ABC vuông tại A.
Vậy chọn đáp án B.
Bài 20 trang 67 SBT Toán 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho ba điểm A(1; 5), B(- 1; - 1), C(2; - 5)
a) Chứng minh ba điểm A, B, C không thẳng hàng.
b) Tìm tọa độ trọng tâm G của tam giác ABC.
c) Tìm tọa độ điểm D sao cho tứ giác ABCD là hình thang có AB // CD và CD=AB.
Lời giải:
a) Ta có: =(-1-1;-1-5)= (-2;-6) và = (2-1;-5-5) = (1;-10)
Ta thấy nên không cùng phương.
Vậy A, B, C không thẳng hàng.
b) Tọa độ trọng tâm G của tam giác ABC:
Vậy .
c) Do tứ giác ABCD là hình thang có AB // CD
Nên và ngược hướng
Mà CD= nên =
Gọi D(a; b), ta có: =(-1-1;-1-5) = (-2;-6), =(a-2b;b+5) .
Suy ra
Vậy D(5; 4).
Bài 21 trang 67 SBT Toán 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(- 2; 4), B(- 5; - 1), C(8; - 2). Giải tam giác ABC (làm tròn các kết quả số đo góc đến hàng đơn vị).
Lời giải:
Ta có: = (-5+2;-1-4) = (-3;-5)
=(8+2;-2-4) = (10;-6)
=(8+5;-2+1) = (13;-1)
Suy ra: AB=||=
AC=||=
BC=||=
Ta có: .= (-3).10+(-5).(-6) = 0 suy ra vuông góc với hay .
Ta có: cos(,)
= 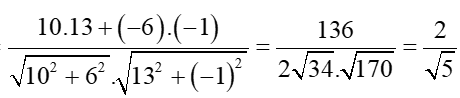
Suy ra .
Bài 22 trang 67 SBT Toán 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho hai điểm A(4; - 2), B(10; 4) và điểm M nằm trên trục Ox. Tìm tọa độ điểm M sao cho || có giá trị nhỏ nhất.
Lời giải:
Do M nằm trên trục Ox nên M(a; 0).
Khi đó = (4-a;-2) và = (10-a;4).
= (14-2a;2)
||
Suy ra ||2 = (14-2a)2 + 2222=4
Giá trị nhỏ nhất của ||2 là 4
Hay giá trị nhỏ nhất của || là 2 đạt được khi 14 – 2a = 0a=7
Vậy M(7; 0).
Bài 23 trang 67 SBT Toán 10 Tập 2: Trên màn hình ra đa của đài kiểm soát không lưu (được coi như mặt phẳng tọa độ Oxy với đơn vị trên các trục tính theo ki-lô-mét), một máy bay trực thăng chuyển động thẳng đều từ thành phố A có tọa độ (600; 200) đến thành phố B có tọa độ (200; 500) và thời gian bay quãng đường AB là 3 giờ. Hãy tìm tọa độ của máy bay trực thăng tại thời điểm sau khi xuất phát 1 giờ.
Lời giải:
Gọi M(a; b) là tọa độ của máy bay trực thăng tại thời điểm sau khi xuất phát 1 giờ.
Ta có: =(a-600;b-200) và =(-400;300)
Do máy bay chuyển động thẳng đều nên quãng đường máy bay đi được sau 1 giờ bằng tổng quãng đường hay AM= AB .
Mà M thuộc đoạn AB nên .
Suy ra
Vậy M .
Lời giải sách bài tập Toán lớp 10 Bài 2: Biểu thức tọa độ của các phép toán vectơ Cánh diều hay khác: