Giải SBT Toán 10 trang 83 Tập 2 Cánh diều

Haylamdo biên soạn giải Sách bài tập Toán 10 trang 83 Tập 2 trong Bài 4: Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng SBT Toán 10 Cánh diều Tập 2 hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 10 trang 83.

Giải SBT Toán 10 trang 83 Tập 2 Cánh diều

Bài 46 trang 83 SBT Toán 10 Tập 2: Có hai tàu điện ngầm A và B chạy trong nội đô thành phố cùng xuất phát từ hai ga, chuyển động đều theo đường thẳng. Trên màn hình ra đa của trạm điều khiển (được coi như mặt phẳng tọa độ Oxy với đơn vị trên các trục tính theo ki-lô-mét), sau khi xuất phát t (giờ) (t ≥ 0), vị trí của tàu A có tọa độ được xác định bởi công thức 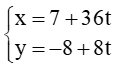, vị trí của tàu B có tọa độ là (9 + 8t; 5 – 36t)

a) Tính côsin góc giữa hai đường đi của hai tàu A và B.

b) Sau bao lâu kể từ thời điểm xuất phát hai tàu gần nhau nhất?

Lời giải:

a) Tàu A có tọa độ được xác định bởi công thức

nên tàu A di chuyển theo hướng của vectơ $\overrightarrow{u_1}$=(36;8)

Vị trí của tàu B có tọa độ là (9 + 8t; 5 – 36t)

Hay tàu B di chuyển theo hướng của vectơ $\overrightarrow{u_2}$=(8;-36)

Ta thấy $\overrightarrow{u_1}.\overrightarrow{u_2}$=36.8+8(-36)=0 nên $\overrightarrow{u_1}$ vuông góc với $\overrightarrow{u_2}$

Vì vậy hai tàu di chuyển vuông góc với nhau.

b) Vị trí của tàu A sau khi xuất phát t giờ là: M(7 + 36t; – 8 – 8t)

Vị trí của tàu B sau khi xuất phát t giờ là: N(9 + 8t; 5 – 36t).

Suy ra $\overrightarrow{MN}$=(2-18t;13-44t)

$\Rightarrow$MN=|$\overrightarrow{MN}$|=$\sqrt{{\left(2-28t\right)}^2+{\left(13-44t\right)}^2}$

$=\sqrt{2720{\left(t-\frac{157}{680}\right)}^2+\frac{4761}{170}}\ge \sqrt{\frac{4761}{170}}\approx 5,29km$

Vậy MN nhỏ nhất là 5,29km khi t = $\frac{157}{680}$ giờ.

Lời giải sách bài tập Toán lớp 10 Bài 4: Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng Cánh diều hay khác:

• Giải SBT Toán 10 trang 81 Tập 2

• Giải SBT Toán 10 trang 82 Tập 2