Giải SBT Toán 10 trang 81 Tập 2 Cánh diều
Haylamdo biên soạn giải Sách bài tập Toán 10 trang 81 Tập 2 trong Bài 4: Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng SBT Toán 10 Cánh diều Tập 2 hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 10 trang 81.
Giải SBT Toán 10 trang 81 Tập 2 Cánh diều
Bài 33 trang 81 SBT Toán 10 Tập 2: Phương trình nào dưới đây là phương trình tham số của một đường thẳng song song với đường thẳng x – 2y + 3 = 0?
A. 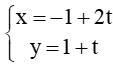
B. 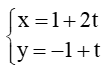
C. 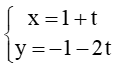
D. 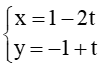
Lời giải:
Gọi d là đường thẳng cần tìm song song với đường thẳng x – 2y + 3 = 0
Do đó d có vectơ pháp tuyến là: =(1;-2).
Do đó d có vectơ chỉ phương là =k(2;1).
Như vậy chỉ có phương án A và B là thỏa mãn có vectơ chỉ phương là =k(2;1). Do đó đáp án C và D sai.
Xét 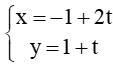
Do đó đường thẳng ở câu A trùng với đường thẳng x – 2y + 3 = 0.
Xét 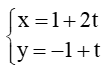
Thay x = 1 và y = - 1 vào phương trình đường thẳng x – 2y + 3 = 0, ta được: 1 – 2.(-1) + 3 = 0 ( vô lí). Do đó đường thẳng ý b song song với đường thẳng x – 2y + 3 = 0.
Vậy chọn đáp án B.
Bài 34 trang 81 SBT Toán 10 Tập 2: Phương trình nào dưới đây là phương trình tham số của một đường thẳng vuông góc với đường thẳng 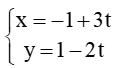
A. 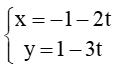
B. 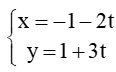
C. 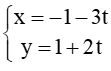
D. 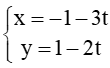
Lời giải:
Xét phương trình đường thẳng 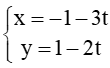
Gọi d là đường thẳng cần tìm vuông góc với đường thẳng đã cho.
Do đó d có vectơ chỉ phương vuông góc với vectơ chỉ phương của đường thẳng đã cho nên vectơ chỉ phương của d là: =k(2;3) với k ∈ℝ.
Xét các đáp án chỉ có đáp án A thỏa mãn có vectơ chỉ phương =(-2;-3) là đúng với k = -1.
Vậy chọn đáp án A.
Bài 35 trang 81 SBT Toán 10 Tập 2: Đường thẳng ∆ đi qua điểm M(- 1; 2) và song song với đường thẳng d: 2x – y – 5 = 0 có phương trình tổng quát là:
A. 2x – y = 0;
B. 2x – y + 4 = 0;
C. 2x + y + 4 = 0;
D. x + 2y – 3 = 0.
Lời giải:
Xét đường thẳng d: 2x – y – 5 = 0 có vectơ pháp tuyến =(2;-1).
Vì ∆ // d nên vectơ pháp tuyến của ∆ là =(2;-1).
Đường thẳng ∆ đi qua M( -1; 2) và nhận =(2;-1) làm vectơ pháp tuyến nên có phương trình tổng quát là: 2(x + 1) – (y – 2) = 0 hay 2x – y + 4 = 0.
Vậy chọn đáp án B.
Bài 36 trang 81 SBT Toán 10 Tập 2: Đường thẳng ∆ đi qua điểm M(3; - 4) và vuông góc với đường thẳng d: x – 3y + 1 = 0 có phương trình tổng quát là:
A. x – 3y – 15 = 0;
B. – 3x + y + 5 = 0;
C. 3x + y – 13 = 0;
D. 3x + y – 5 = 0.
Lời giải:
Đường thẳng ∆ vuông góc với đường thẳng d: x – 3y + 1 = 0
Nên đường thẳng ∆ có vectơ pháp tuyến là: =(3;1).
Đường thẳng ∆ đi qua M(3; - 4) nên có phương trình tổng quát là:
3(x - 3) + (y + 4) = 0 hay 3x + y - 5 = 0.
Vậy chọn đáp án D.
Bài 37 trang 81 SBT Toán 10 Tập 2: Cho ∆1: x – 2y + 3 = 0 và ∆2: – 2x – y + 5 = 0. Số đo góc giữa hai đường thẳng ∆1 và ∆2 là:
A. 300;
B. 450;
C. 900;
D. 600.
Lời giải:
Ta thấy vectơ pháp tuyến của là: =(1;-2)
Vectơ pháp tuyến của là: =(-2;-1)
Ta có: = 1.(-2)+(-2).(-1)=0
Suy ra vuông góc với
Vậy 2 đường thẳng trên vuông góc với nhau, chọn đáp án C.
Lời giải sách bài tập Toán lớp 10 Bài 4: Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng Cánh diều hay khác:

