Giải SBT Toán 10 trang 90 Tập 2 Cánh diều

Haylamdo biên soạn giải Sách bài tập Toán 10 trang 90 Tập 2 trong Bài 5: Phương trình đường tròn SBT Toán 10 Cánh diều Tập 2 hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 10 trang 90.

Giải SBT Toán 10 trang 90 Tập 2 Cánh diều

Bài 57 trang 90 SBT Toán 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho các đường thẳng: ${\Delta }_1$: x+y+1=0, ${∆}_2$: 3x+4y+20=0; ${∆}_3$: 2x-y+50=0 và đường tròn (C); (x+3)²+(y-1)²=9 . Xác định vị trí tương đối của các đường thẳng đã cho đối với đường tròn (C).

Lời giải:

Đường tròn (C) có tâm I(-3; 1) và bán kính R = 3.

Ta có: d(I,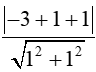${\Delta }_1$)=<3, suy ra ${\Delta }_1$ cắt đường tròn tại hai điểm phân biệt.

d(I,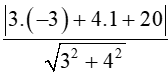${∆}_2$)==$\frac{15}{5}$=3=R, suy ra ${∆}_2$ tiếp xúc với đường tròn.

d(I,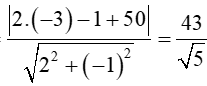${∆}_3$)=>3, suy ra ${∆}_3$ không có điểm chung với đường tròn.

Bài 58 trang 90 SBT Toán 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho điểm M(1; 1) và đường thẳng ∆: 3x + 4y + 3 = 0. Viết phương trình đường tròn (C), biết (C) có tâm M và đường thẳng ∆ cắt (C) tại hai điểm N, P thỏa mãn tam giác MNP đều.

Lời giải:

Gọi H là hình chiếu của M lên ∆

Suy ra MH là khoảng cách từ M đến ∆

MH = 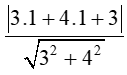=2

Xét tam giác MNH vuông tại H có:

MN = $\frac{MH}{\sin {60}^o}=\frac{4}{\sqrt{3}}$

Mà R = MN = $\frac{4}{\sqrt{3}}$

Phương trình đường tròn là: (x-1)² +(y-1)² =$\frac{16}{3}$.

Lời giải sách bài tập Toán lớp 10 Bài 5: Phương trình đường tròn Cánh diều hay khác:

• Giải SBT Toán 10 trang 88 Tập 2

• Giải SBT Toán 10 trang 89 Tập 2