Cho hàm số bậc hai có đồ thị là parabol có đỉnh S, đi qua các điểm A, B, C(0; – 1) SBT Toán 10 Tập 1
Giải SBT Toán 10 Bài 2: Hàm số bậc hai
Haylamdo biên soạn và sưu tầm lời giải Bài 2 trang 55 SBT Toán 10 Tập 1 trong Bài 2: Hàm số bậc hai. Với lời giải chi tiết nhất hy vọng sẽ giúp các bạn dễ dàng nắm được cách làm bài tập Sách bài tập Toán 10.
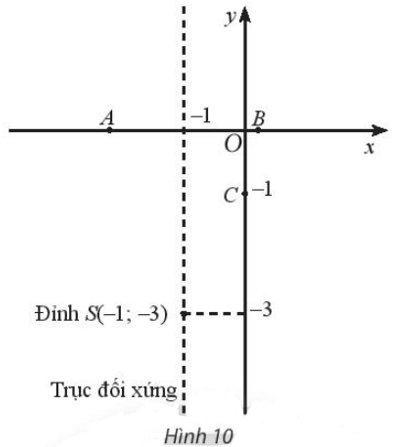
Bài 2 trang 55 SBT Toán 10 Tập 1: Cho hàm số bậc hai có đồ thị là parabol có đỉnh S, đi qua các điểm A, B, C(0; – 1) được cho trong Hình 10.
a) Vẽ đồ thị hàm số đã cho;
b) Tìm tập giá trị của hàm số và chỉ ra các khoảng biến thiên của hàm số.
Lời giải:
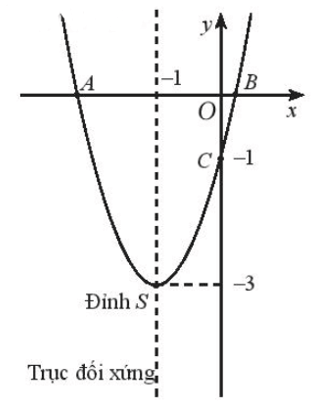
a) Ta vẽ parabol có bề lõm hướng lên trên và đi qua các điểm A, S, C, B, ta được đồ thị của hàm số đã cho như sau:
b) Đồ thị hàm số đã cho là parabol quay bề lõm lên trên nên hàm số có giá trị nhỏ nhất bằng tung độ đỉnh của parabol.
Từ đồ thị, ta có đỉnh S có tọa độ (– 1; – 3). Suy ra hàm số có tập giá trị là [– 3; + ∞).
Quan sát đồ thị ta thấy đồ thị đi xuống từ trái qua phải trên khoảng (– ∞; – 1) nên hàm số nghịch biến trên khoảng (– ∞; – 1) và đồ thị đi lên từ trái qua phải trên khoảng (– 1; + ∞) nên hàm số đồng biến trên khoảng (– 1; + ∞).