Tìm khoảng biến thiên và tập giá trị của các hàm số sau f(x)=-2x^2 - 4x + 7 SBT Toán 10 Tập 1

Giải SBT Toán 10 Bài 2: Hàm số bậc hai

Haylamdo biên soạn và sưu tầm lời giải Bài 5 trang 55 SBT Toán 10 Tập 1 trong Bài 2: Hàm số bậc hai. Với lời giải chi tiết nhất hy vọng sẽ giúp các bạn dễ dàng nắm được cách làm bài tập Sách bài tập Toán 10.

Bài 5 trang 55 SBT Toán 10 Tập 1: Tìm khoảng biến thiên và tập giá trị của các hàm số sau:

a) y = f(x) = – 2x² – 4x + 7;

b) y = f(x) = x² – 6x + 1.

Lời giải:

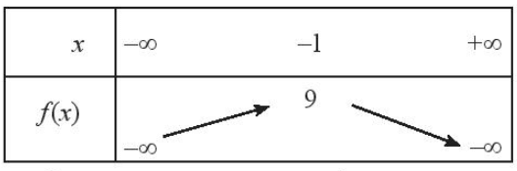
a) Hàm số y = f(x) = – 2x² – 4x + 7 có a = – 2 < 0 và đồ thị của hàm số là parabol có tọa độ đỉnh S là x_S = $-\frac{b}{2a}=-\frac{-4}{2.\left(-2\right)}=-1$ , y_S = – 2 . (– 1)² – 4 . (– 1) + 7 = 9 hay S(– 1; 9).

Ta có bảng biến thiên:

Vậy hàm số đồng biến trên (– ∞; – 1) và nghịch biến trên (– 1; + ∞).

Hàm số có tập giá trị là T = (– ∞; 9].

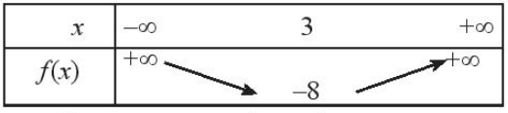
b) Hàm số y = f(x) = x² – 6x + 1 có a = 1 > 0 và đồ thị hàm số là parabol có tọa độ đỉnh S là $x_S=-\frac{b}{2a}=-\frac{-6}{2.1}=3$ , y_S = 3² – 6 . 3 + 1 = – 8 hay S(3; – 8).

Ta có bảng biến thiên:

Vậy hàm số nghịch biến trên (– ∞; 3) và đồng biến trên (3; + ∞).

Hàm số có tập giá trị là T = [– 8; + ∞).