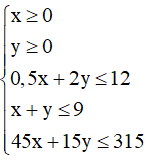Trong một cuộc thi pha chế, mỗi đội chơi được sử dụng tối đa 12 g hương liệu, 9 lít nước và 315 g đường
Trong một cuộc thi pha chế, mỗi đội chơi được sử dụng tối đa 12 g hương liệu, 9 lít nước và 315 g đường để pha chế hai loại nước A và B. Để pha chế 1 lít nước A cần 45 g đường, 1 lít nước và 0,5 g hương liệu; để pha chế 1 lít nước B cần 15 g đường, 1 lít nước và 2 g hương liệu. Mỗi lít nước A nhận được 60 điểm thưởng, mỗi lít nước B nhận được 80 điểm thưởng. Hỏi cần pha chế bao nhiêu lít nước mỗi loại để đội chơi được số điểm thưởng là cao nhất?
Giải sách bài tập Toán lớp 10 Bài 4: Hệ bất phương trình bậc nhất hai ẩn
Bài 2.9 trang 23 sách bài tập Toán lớp 10 Tập 1: Trong một cuộc thi pha chế, mỗi đội chơi được sử dụng tối đa 12 g hương liệu, 9 lít nước và 315 g đường để pha chế hai loại nước A và B. Để pha chế 1 lít nước A cần 45 g đường, 1 lít nước và 0,5 g hương liệu; để pha chế 1 lít nước B cần 15 g đường, 1 lít nước và 2 g hương liệu. Mỗi lít nước A nhận được 60 điểm thưởng, mỗi lít nước B nhận được 80 điểm thưởng. Hỏi cần pha chế bao nhiêu lít nước mỗi loại để đội chơi được số điểm thưởng là cao nhất?
Lời giải:
Gọi số lít nước A và B cần pha chế lần lượt là x lít và y lít (x ≥ 0; y ≥ 0).
Do 1 lít nước A cần 45 g đường, 1 lít nước và 0,5 g hương liệu nên x lít nước A cần 45x g đường, x lít nước và 0,5x g hương liệu.
Do 1 lít nước B cần 15 g đường, 1 lít nước và 2 g hương liệu nên y lít nước A cần 15y g đường, y lít nước và 2y g hương liệu.
Do có tối đa 12g hương liệu, 9 lít nước và 315 g đường nên 45x + 15y ≤ 315; x + y ≤ 9 và 0,5x + 2y ≤ 12.
Khi đó ta có hệ bất phương trình
Với số điểm thưởng đội chơi nhận được là F(x; y) = 60x + 80y (điểm).
Biểu diễn tập nghiệm của các bất phương trình trên mặt phẳng tọa độ:
• Đường thẳng d1: x = 0 là đường thẳng trùng với trục Oy.
Chọn điểm I(1; 1)∉ d1 và thay bảo biểu thức x ta được 1 > 0.
Suy ra miền nghiệm của bất phương trình x ≥ 0 là nửa mặt phẳng bờ d1 chứa điểm I(1; 1).
• Đường thẳng d2: y = 0 là đường thẳng trùng với trục Ox.
Chọn điểm I(1; 1) ∉ d2 và thay bảo biểu thức y ta được 1 > 0.
Suy ra miền nghiệm của bất phương trình y ≥ 0 là nửa mặt phẳng bờ d2 chứa điểm I(1; 1).
• Vẽ đường thẳng d3: 0,5x + 2y = 12 bằng cách vẽ đường thẳng đi qua hai điểm (0; 6) và (4; 5).
Chọn điểm I(1; 1)∉ d3 và thay bảo biểu thức 0,5x + 2y ta được 0,5 . 1 + 2 . 1 = 2,5 < 12.
Suy ra miền nghiệm của bất phương trình 0,5x + 2y ≤ 12 là nửa mặt phẳng bờ d3 chứa điểm I(1; 1).
• Vẽ đường thẳng d4: x + y = 9 bằng cách vẽ đường thẳng đi qua hai điểm (3; 6) và (4; 5).
Chọn điểm I(1; 1) ∉ d4 và thay bảo biểu thức x + y ta được 1 + 1 = 2 < 9.
Suy ra miền nghiệm của bất phương trình x + y ≤ 9 là nửa mặt phẳng bờ d4 chứa điểm I(1; 1).
• Vẽ đường thẳng d5: 45x + 15y = 315 bằng cách vẽ đường thẳng đi qua hai điểm (5; 6) và (7; 0).
Chọn điểm I(1; 1) ∉ d4 và thay bảo biểu thức 45x + 15y ta được 45 . 1 + 15. 1 = 60 < 315.
Suy ra miền nghiệm của bất phương trình 45x + 15y ≤ 315 là nửa mặt phẳng bờ d5 chứa điểm I(1; 1).
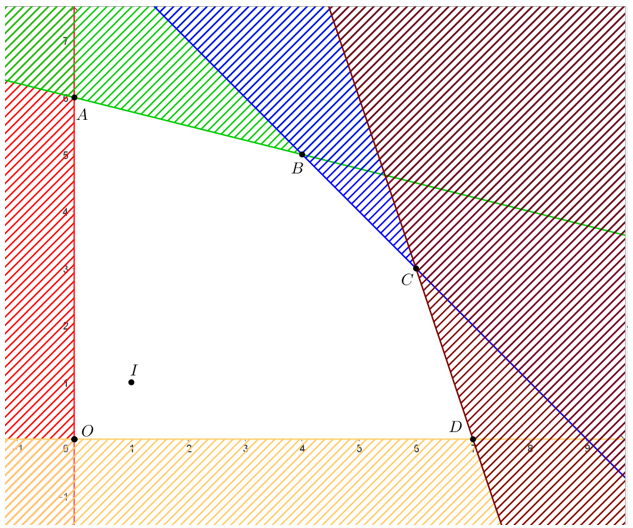
Khi đó miền nghiệm của hệ bất phương trình là miền không bị gạch như hình vẽ dưới đây
Miền nghiệm của hệ là miền ngũ giác ABCDO với A(0; 6), B(4; 5), C(6; 3), D(7; 0) và O(0; 0).
Ta có F(0; 6) = 60 . 0 + 80 . 6 = 480;
F(4; 5) = 60 . 4 + 80 . 5 = 640;
F(6; 3) = 60 . 6 + 80 . 3 = 600;
F(7; 0) = 60 . 7 + 80 . 0 = 420;
F(0; 0) = 0.
Giá trị lớn nhất là F(4; 5) = 640.
Vậy cần pha 4 lít nước loại A và 5 lít nước loại B để số điểm thưởng nhận được là lớn nhất.
