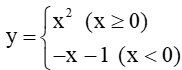Vẽ đồ thị của các hàm số sau và chỉ ra tập giá trị, các khoảng đồng biến

Vẽ đồ thị của các hàm số sau và chỉ ra tập giá trị, các khoảng đồng biến, nghịch biến của chúng.

Sách bài tập Toán 10 Kết nối tri thức Bài 15: Hàm số

Bài 6.6 trang 8 Sách bài tập Toán lớp 10 Tập 2: Vẽ đồ thị của các hàm số sau và chỉ ra tập giá trị, các khoảng đồng biến, nghịch biến của chúng.

a) $y=-\frac{1}{2}x+5$;

b) y = 3x²;

c)

Lời giải:

a)

Xét hàm số $y=-\frac{1}{2}x+5$

Ta có:

Khi x = 0 thì $y=-\frac{1}{2}.0+5=5$

Khi x = 10 thì $y=-\frac{1}{2}.10+5=0$

Do đó, đồ thị hàm số là đường thẳng đi qua hai điểm (0; 5) và (10; 0).

Ta có hình vẽ đồ thị hàm số:

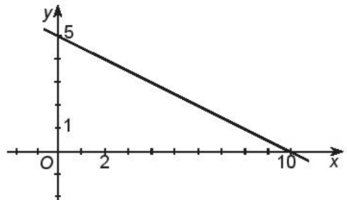
Tập giá trị của hàm số là: T = ℝ.

Đồ thị hàm số luôn đi xuống từ trái sang phải do đó hàm số nghịch biến trên ℝ.

b)

Xét hàm số y = 3x²

Ta có:

Trục đối xứng: x = 0

Đỉnh parabol là: (0; 0)

Khi x = 1 thì y = 3.1² = 3

Khi x = –1 thì y = 3.(–1)² = 3

Do đó, đồ thị hàm số là parabol có đỉnh (0; 0) đi qua hai điểm (1; 3) và (–1; 3)

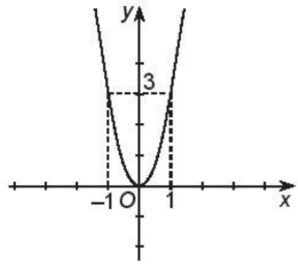
Tập xác định của hàm số là: T = [0; +∞).

Đồ thị hàm số đi xuống từ trái sang phải trên khoảng (–∞; 0) nên hàm số nghịch biến trên khoảng (–∞; 0).

Đồ thị hàm số đi lên từ trái sang phải trên khoảng (0; +∞) nên hàm số đồng biến trên khoảng (0; +∞).

c)

Xét hàm số

+) Khi x ≥ 0, ta có:

y = x²

Do đó, đồ thị hàm số là nửa parabol có trục đối xứng x = 0, đỉnh (0; 0), đi qua điểm (1; 1).

+) Khi x < 0, ta có:

y = –x – 1

Do đó, đồ thị hàm số là một phần đường thẳng đi qua điểm (0; –1) và (–1; 0).

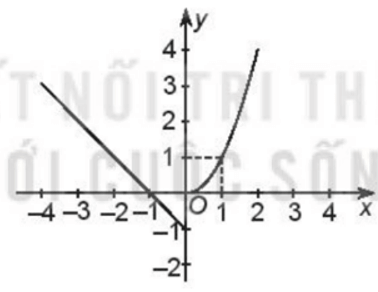
Tập giá trị của hàm số là: T = (–1; +∞)

Đồ thị hàm số đi xuống từ trái sang phải trên khoảng (–∞; 0) nên hàm số nghịch biến trên khoảng (–∞; 0)

Đồ thị hàm số đi lên từ trái sang phải trên khoảng (0; +∞) nên hàm số đồng biến trên khoảng (0; +∞).