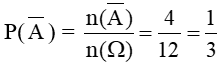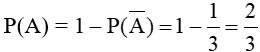Có ba chiếc hộp trong đó hộp I có một viên bi đỏ, một viên bi xanh

Có ba chiếc hộp trong đó hộp I có một viên bi đỏ, một viên bi xanh, một viên bi vàng; hộp II có một viên bi xanh, một viên bi vàng, hộp III có một viên bi đỏ và một viên bi xanh. Tất cả các viên bi đều có cùng kích thước. Từ mỗi hộp rút ngẫu nhiên một viên bi.

Sách bài tập Toán 10 Kết nối tri thức Bài 27: Thực hành tính xác suất theo định nghĩa cổ điển

Bài 9.9 trang 66 Sách bài tập Toán lớp 10 Tập 2: Có ba chiếc hộp trong đó hộp I có một viên bi đỏ, một viên bi xanh, một viên bi vàng; hộp II có một viên bi xanh, một viên bi vàng, hộp III có một viên bi đỏ và một viên bi xanh. Tất cả các viên bi đều có cùng kích thước. Từ mỗi hộp rút ngẫu nhiên một viên bi.

a) Vẽ sơ đồ hình cây mô tả các phần tử của không gian mẫu.

b) Tính xác suất để trong ba viên bi rút ra có ít nhất một viên bi đỏ bằng cách tính gián tiếp thông qua tính xác suất của biến cố đối.

Lời giải:

a)

Kí hiệu Đ, X, V tương ứng là viên bi màu đỏ, xanh, vàng.

Ta có sơ đồ hình cây mô tả các phần tử của không gian mẫu:

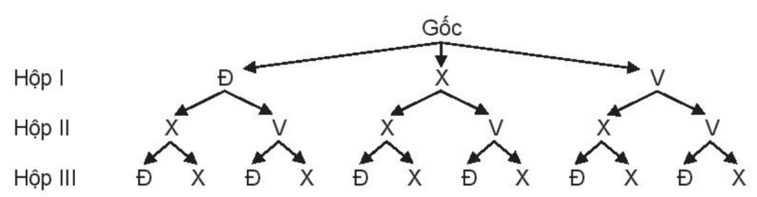
Do đó, ta có:

Ω = {(ĐXĐ; ĐXX; ĐVĐ; ĐVX; XXĐ; XXX; XVĐ; XVX; VXĐ; VXX; VVĐ; VVX}.

Vậy n(Ω) = 12.

b)

Gọi biến cố A: “Trong ba viên bi rút ra có ít nhất một viên bi đỏ”

Biến cố đối của A là 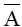: “Trong ba viên bi rút ra không có viên bi màu đỏ”.

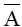
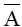
Ta có: = {XXX; XVX; VXX; VVX}; n() = 4.

Do đó, ta có:

Vậy