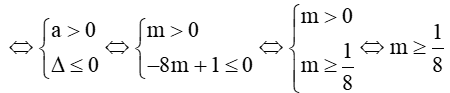Giải SBT Toán 10 trang 25 Tập 2 Kết nối tri thức

---

Với Giải SBT Toán 10 trang 25 Tập 2 trong Bài tập cuối chương 6 Sách bài tập Toán 10 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 10 trang 25.

Giải SBT Toán 10 trang 25 Tập 2 Kết nối tri thức

Bài 6.47 trang 25 Sách bài tập Toán lớp 10 Tập 2: Tập nghiệm của bất phương trình x² – 4x + 3 < 0 là

A. (1; 3);

B. (–∞; 1)∪[3; +∞);

C. [1; 3];

D. (–∞; 1]∪[4; +∞).

Hướng dẫn giải:

Đáp án đúng là: A

x² – 4x + 3 < 0 (*)

Xét tam thức f(x) = x² – 4x + 3 < 0 có:

a = 1 > 0

Δ = (–4)² – 4.1.3 = 4 > 0

f(x) = x² – 4x + 3 = 0 ⇔ x₁ = 1; x₂ = 3

Do đó, x² – 4x + 3 < 0 ⇔ 1 < x < 3.

Vậy tập nghiệm của bất phương trình (*) là: (1; 3).

Bài 6.48 trang 25 Sách bài tập Toán lớp 10 Tập 2: Các giá trị của tham số m làm cho biểu thức f(x) = x² + 4x + m – 5 luôn dương là

A. m ≥ 9;

B. m > 9;

C. Không có m;

D. m < 9.

Hướng dẫn giải:

Đáp án đúng là: B

Xét tam thức f(x) = x² + 4x + m – 5 có:

a = 1 > 0

f(x) luôn dương ⇔ Δ < 0

⇔ 4² – 4.1.(m – 5) < 0

⇔ 16 – 4m + 20 < 0

⇔ 4m > 36

⇔ m > 9.

Bài 6.49 trang 25 Sách bài tập Toán lớp 10 Tập 2: Phương trình (m + 2) x² – 3x + 2m – 3 = 0 có hai nghiệm trái dấu khi và chỉ khi

A. m < –2 hoặc $m>\frac{3}{2}$;

B. $m>\frac{3}{2}$;

C. $-2<m<\frac{3}{2}$;

D. m < 2.

Hướng dẫn giải:

Đáp án đúng là: C

Phương trình (m + 2) x² – 3x + 2m – 3 = 0 có hai nghiệm trái dấu khi và chỉ khi

ac < 0

⇔ (m + 2)(2m – 3) < 0

⇔ 2m² – 3m + 4m – 6 < 0

⇔ 2m² + m – 6 < 0

Xét tam thức f(x) = 2m² + m – 6 có:

a = 2 > 0

Δ = 1² – 4.1.(–6) = 25 > 0

f(x) = 2m² + m – 6 = 0 có hai nghiệm là: x₁ = –2; x₂ = $\frac{3}{2}$.

Do đó, 2m² + m – 6 < 0 ⇔ –2 < x < $\frac{3}{2}$

Vậy phương trình (m + 2) x² – 3x + 2m – 3 = 0 có hai nghiệm trái dấu khi và chỉ khi $-2<m<\frac{3}{2}$.

Bài 6.50 trang 25 Sách bài tập Toán lớp 10 Tập 2: Bất phương trình mx² – (2m – 1)x + m + 1 < 0 vô nghiệm khi và chỉ khi

A. $m\le \frac{1}{8}$;

B. $m>\frac{1}{8}$;

C. $m<\frac{1}{8}$;

D. $m\ge \frac{1}{8}$.

Hướng dẫn giải:

Đáp án đúng là: D

+) Khi m = 0, ta có:

mx² – (2m – 1)x + m + 1 < 0

⇔ x + 1 < 0

⇔ x < –1

Do đó, m = 0 không thỏa mãn yêu cầu đề bài

+) Khi m ≠ 0, ta có:

Xét tam thức: f(x) = mx² – (2m – 1)x + m + 1 có:

a = m,

∆ = [–(2m – 1)²] – 4.m.(m + 1) = 4m² – 4m + 1 – 4m² – 4m = –8m + 1

Để mx² – (2m – 1)x + m + 1 < 0 vô nghiệm khi và chỉ khi mx² – (2m – 1)x + m + 1 ≥ 0 với mọi số thực x

Vậy khi $m\ge \frac{1}{8}$ thì bất phương trình mx² – (2m – 1)x + m + 1 < 0 vô nghiệm.

Bài 6.51 trang 25 Sách bài tập Toán lớp 10 Tập 2: Số nghiệm của phương trình $\sqrt{x^2+4x-2}=x-3$ là

A. 0;

B. 1;

C. 2;

D. 3.

Hướng dẫn giải:

Đáp án đúng là: A

$\sqrt{x^2+4x-2}=x-3$ (*)

Bình phương hai vế (*) ta có:

x² + 4x – 2 = (x – 3)²

⇔x² + 4x – 2 = x² – 6x + 9

⇔ 10x = 11

⇔ $x=\frac{11}{10}$

Thay $x=\frac{11}{10}$ vào (*) ta có:

$\sqrt{{\left(\frac{11}{10}\right)}^2+4.\frac{11}{10}-2}=\frac{11}{10}-3\iff \frac{19}{10}=-\frac{19}{10}$ (không thỏa mãn)

Vậy phương trình (*) vô nghiệm.

Bài 6.52 trang 25 Sách bài tập Toán lớp 10 Tập 2: Tập nghiệm của phương trình $\sqrt{2x^2-9x-9}=3-x$ là

A. S = {6};

B. S = ∅;

C. S = {–3};

D. S = {–3; 6}.

Hướng dẫn giải:

Đáp án đúng là: C

$\sqrt{2x^2-9x-9}=3-x$ (*)

Bình phương hai vế (*) ta có:

2x² – 9x – 9 = (3 – x)²

⇔2x² – 9x – 9 = 9 – 6x + x²

⇔ x² – 3x – 18 = 0

⇔ x = 6 hoặc x = –3

Thay x = 6 vào (*) ta có:

$\sqrt{2.6^2-9.6-9}=3-6\iff 3=-3$ (không thỏa mãn)

Thay x = –3 vào (*) ta có:

$\sqrt{2.{(-3)}^2-9.(-3)-9}=3-(-3)\iff 6=6$ (thỏa mãn)

Vậy tập nghiệm của phương trình (*) là: S = {–3}.

Bài 6.53 trang 25 Sách bài tập Toán lớp 10 Tập 2: Tập nghiệm của phương trình $\sqrt{2x^2-5x+1}=\sqrt{x^2+2x-9}$ là

A. S = {2};

B. S = {5};

C. S = ∅;

D. S = {2; 5}.

Hướng dẫn giải:

Đáp án đúng là: B

$\sqrt{2x^2-5x+1}=\sqrt{x^2+2x-9}$ (*)

Bình phương hai vế của (*) ta có:

2x² – 5x + 1 = x² + 2x – 9

⇔ x² – 7x + 10 = 0

⇔ x = 5 hoặc x = 2

Thay x = 5 vào (*) ta có:

$\sqrt{2.5^2-5.5+1}=\sqrt{5^2+2.5-9}\iff \sqrt{26}=\sqrt{26}$ (thỏa mãn)

Thay x = 2 vào (*) ta có:

$\sqrt{2.2^2-5.2+1}=\sqrt{2^2+2.2-9}\iff \sqrt{-1}=\sqrt{-1}$ (không thể tồn tại)

Vậy tập nghiệm của phương trình (*) là: S = {5}.

Bài 6.54 trang 25 Sách bài tập Toán lớp 10 Tập 2: Tìm tập xác định của các hàm số sau:

a) $y=\sqrt{-x^2+3x-2}$;

b) $y=\frac{x-1}{\sqrt{x^2-1}}$.

Hướng dẫn giải:

a)

Điều kiện xác định của hàm số là: –x² + 3x – 2 ≥ 0

Xét tam thức f(x) = –x² + 3x – 2 có:

a = –1 < 0

∆ = 3² – 4.(–1).(–2) = 1 > 0

f(x) = 0 có hai nghiệm phân biệt là: x₁ = 2 ; x₂ = 1

Do đó, ta có:

–x² + 3x – 2 ≥ 0

⇔ 1 ≤ x ≤ 2

Vậy tập xác định của hàm số là: D = [1; 2].

b)

Điều kiện xác định của hàm số là:

x² – 1 > 0

⇔ x² > 1

⇔ x < –1 hoặc x > 1

Vậy tập xác định của hàm số là: D = (–∞; –1)∪(1; +∞).

Lời giải sách bài tập Toán lớp 10 Bài tập cuối chương 6 Kết nối tri thức hay khác:

• Giải SBT Toán 10 trang 22 Tập 2

• Giải SBT Toán 10 trang 23 Tập 2

• Giải SBT Toán 10 trang 24 Tập 2

• Giải SBT Toán 10 trang 26 Tập 2

• Giải SBT Toán 10 trang 27 Tập 2