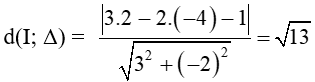Giải SBT Toán 10 trang 41 Tập 2 Kết nối tri thức
Với Giải SBT Toán 10 trang 41 Tập 2 trong Bài 21: Đường tròn trong mặt phẳng tọa độ Sách bài tập Toán 10 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 10 trang 41.
Giải SBT Toán 10 trang 41 Tập 2 Kết nối tri thức
Bài 7.19 trang 41 Sách bài tập Toán lớp 10 Tập 2: Tìm tâm và bán kính của đường tròn (C) trong các trường hợp sau:
a) (x – 2)2 + (y – 8)2 = 49;
b) (x + 3)2 + (y – 4)2 = 23.
Hướng dẫn giải:
Phương trình đường tròn có dạng: (x – a)2 + (y – b)2 = R2
Với (a; b) là tọa độ tâm I và R > 0 là bán kính của đường tròn
a)
Xét (x – 2)2 + (y – 8)2 = 49 có:
a = 2, b = 8, R2 = 49 ⇒ R = 7
Vậy đường tròn (C) có tâm I(2; 8) và bán kính R = 7.
b)
Xét(x + 3)2 + (y – 4)2 = 23 có:
a = –3, b = 4, R2 = 23 ⇒ R =
Vậy đường tròn (C) có tâm I(–3; 4) và bán kính R = .
Bài 7.20 trang 41 Sách bài tập Toán lớp 10 Tập 2: Phương trình nào dưới đây là phương trình của một đường tròn? Khi đó hãy tìm tâm và bán kính của nó.
a) x2 + 2y2 – 4x – 2y + 1 = 0.
b) x2 + y2 – 4x + 3y + 2xy = 0.
c) x2 + y2 – 8x – 6y + 26 = 0.
d) x2 + y2 + 6x – 4y + 13 = 0
e) x2 + y2 – 4x + 2y + 1 = 0.
Hướng dẫn giải:
a)
Phương trình đã cho không là phương trình của đường tròn do hệ số của x2 và y2 không bằng nhau
b)
Phương trình đã cho không là phương trình của đường tròn do trong phương trình của đường tròn không có thành phần tích xy.
c)
Phương trình đã cho có các hệ số a = 4, b = 3, c = 26, ta có:
a2 + b2 – c = 42 + 32 – 26 = –1 < 0
do đó nó không là phương trình của đường tròn.
d)
Phương trình đã cho có các hệ số a = –3, b = 2, c = 13, ta có:
a2 + b2 – c = (–3)2 + 22 – 13 = 0
do đó nó không là phương trình của đường tròn.
e)
Phương trình đã cho có các hệ số a = 2, b = –1, c = 1, ta có:
a2 + b2 – c = 22 + (–1)2 – 1 = 4 > 0
nên đây là phương trình của đường tròn có tâm I(2; –1) và có bán kính .
Bài 7.21 trang 41 Sách bài tập Toán lớp 10 Tập 2: Viết phương trình của đường tròn (C) trong các trường hợp sau.
a) Có tâm I(3; 1) và có bán kính R = 2.
b) Có tâm I(3; 1) và đi qua điểm M(–1; 7).
c) Có tâm I(2; –4) và tiếp xúc với đường thẳng Δ: 3x – 2y – 1 = 0.
d) Có đường kính AB với A(4; 1), B(–2; –5).
Hướng dẫn giải:
a)
Phương trình đường tròn có tâm I(3; 1) và có bán kính R = 2 là:
(x – 3)2 + (y – 1)2 = 22
⇔ (x – 3)2 + (y – 1)2 = 4.
b)
Đường tròn có tâm I(3; 1) và đi qua điểm M(–1; 7) có bán kính
R = IM =
Phương trình đường tròn có tâm I(3; 1) và đi qua điểm M(–1; 7) là:
(x – 3)2 + (y – 1)2 = ()2
⇔ (x – 3)2 + (y – 1)2 = 52.
c)
Đường tròn có tâm I(2; –4) và tiếp xúc với đường thẳng Δ: 3x – 2y – 1 = 0 có bán kính R =
Phương trình đường tròn có tâm I(2; –4) và tiếp xúc với đường thẳng Δ: 3x – 2y – 1 = 0 là:
(x – 2)2 + (y + 4)2 = ()2
⇔ (x – 2)2 + (y + 4)2 = 13.
d)
Đường tròn có đường kính AB với A(4; 1), B(–2; –5) có:
Tâm I là trung điểm AB nên:
xI = (xA + xB) : 2 = (4 + (– 2)) : 2 = 1
yI = (yA + yB) : 2 = (1 + (– 5)) : 2 = –2
Do đó, I(1; –2).
Bán kính R =
Phương trình đường tròn có đường kính AB với A(4; 1), B(–2; –5) là:
(x – 1)2 + (y + 2)2 = ()2
⇔ (x – 1)2 + (y + 2)2 = 18.
Bài 7.22 trang 41 Sách bài tập Toán lớp 10 Tập 2: Viết phương trình đường tròn (C) có tâm thuộc đường thẳng Δ: x + y – 1 = 0 và đi qua hai điểm A(6; 2), B(–1; 3).
Hướng dẫn giải:
Dựa vào Δ: x + y – 1 = 0 ta có: y = 1 – x
Gọi I là tâm của đường tròn (C). Ta có I ∈ Δ ⇔ I(t; 1 – t)
Vì A, B thuộc (C) nên ta có
AI2 = BI2
⇔ (t – 6)2 + (1 – t – 2)2 = (t + 1)2 + (1 – t – 3)2
⇔ (t – 6)2 + (–1 – t )2 = (t + 1)2 + (–2 – t )2
⇔ (t – 6)2 + (t + 1)2 = (t + 1)2 + (t + 2)2
⇔ (t – 6)2 = (t + 2)2
⇔ t2 – 12t + 36 = t2 + 4t + 4
⇔ 16t = 32
⇔ t = 2
Do đó, I(2; –1)
Bán kính của (C) là:
Phương trình của đường tròn (C) là:
(x – 2)2 + (y + 1)2 = 52
⇔ (x – 2)2 + (y + 1)2 = 25.
Lời giải sách bài tập Toán lớp 10 Bài 21: Đường tròn trong mặt phẳng tọa độ Kết nối tri thức hay khác: