Giải SBT Toán 10 trang 42 Tập 2 Kết nối tri thức
Với Giải SBT Toán 10 trang 42 Tập 2 trong Bài 21: Đường tròn trong mặt phẳng tọa độ Sách bài tập Toán 10 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 10 trang 42.
Giải SBT Toán 10 trang 42 Tập 2 Kết nối tri thức
Bài 7.23 trang 42 Sách bài tập Toán lớp 10 Tập 2: Cho đường tròn (C) có phương trình x2 + y2 + 6x – 4y – 12 = 0. Viết phương trình tiếp tuyến Δ của (C) tại điểm M(0; –2).
Hướng dẫn giải:
Xét đường tròn (C) có phương trình: x2 + y2 + 6x – 4y – 12 = 0. Ta có:
Tâm I(a; b) với a = 6 : (–2) = –3, b = –4 : (–2) = 2, do đó, đường tròn (C) có tâm I(–3; 2).
Đường thẳng Δ đi qua điểm M(0; –2) và có vectơ pháp tuyến là . Phương trình của Δ là
3(x – 0) – 4(y + 2) = 0
⇔ 3x – 4y – 8 = 0.
Bài 7.24 trang 42 Sách bài tập Toán lớp 10 Tập 2: Cho điểm A(4; 2) và hai đường thẳng d: 3x + 4y – 20 = 0, d’: 2x + y = 0.
a) Viết phương trình đường thẳng Δ đi qua A và vuông góc với d.
b) Viết phương trình đường tròn (C) có tâm thuộc đường thẳng d' và tiếp xúc với d tại điểm A.
Hướng dẫn giải:
a)
Dựa vào đề bài ta có do đường thẳng Δ vuông góc với d nên: .
Phương trình của Δ là:
4(x – 4) – 3(y – 2) = 0
⇔ 4x – 3y – 10 = 0.
b)
Gọi I là tâm của đường tròn (C).
Vì d tiếp xúc với (C) tại điểm A nên ta có IA ⊥ d, do đó I thuộc Δ. Mặt khác, I thuộc đường thẳng d'. Suy ra toạ độ của I thoả mãn hệ phương trình
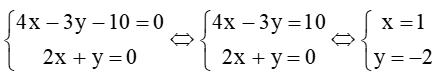
Do đó, I(1; –2)
Bán kính của (C) là:
Vậy phương trình của (C) là
(x – 1)2 + (y + 2)2 = 52
⟺ (x – 1)2 + (y + 2)2 = 25.
Bài 7.25 trang 42 Sách bài tập Toán lớp 10 Tập 2: Cho đường tròn (C), đường thẳng Δ có phương trình lần lượt là:
(x – 1)2 + (y + 1)2 = 2; x + y + 2 = 0.
a) Chứng minh rằng Δ là một tiếp tuyến của đường tròn (C).
b) Viết phương trình tiếp tuyến d của (C), biết rằng d song song với đường thẳng Δ.
Hướng dẫn giải:
Đường tròn (C): (x – 1)2 + (y + 1)2 = 2 có
tâm I(1; –1)
bán kính R2 = 2 ⇒ R = .
a)
Khoảng cách từ I đến đường thẳng Δ là
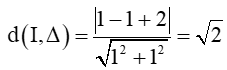
Ta có d(I, Δ) = R, do đó Δ là một tiếp tuyến của (C).
b)
Vì đường thẳng d song song với đường thẳng Δ nên phương trình đường thẳng d có dạng x + y + m = 0, trong đó m ≠ 2.
Để d là tiếp tuyến của (C) khi và chỉ khi
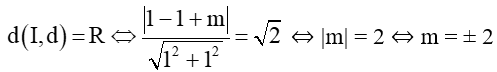
Mà m ≠ 2 nên m = –2
Vậy phương trình của đường thẳng d là x + y – 2 = 0.
Bài 7.26 trang 42 Sách bài tập Toán lớp 10 Tập 2: Cho đường thẳng Δ: x . sinα° + y . cosα° – 1 = 0, trong đó α là một số thực thuộc khoảng (0; 180).
a) Tính khoảng cách từ gốc toạ độ O đến đường thẳng Δ.
b) Chứng minh rằng khi α thay đổi, tồn tại một đường tròn cố định luôn tiếp xúc với đường thẳng Δ.
Hướng dẫn giải:
a)
Khoảng cách từ O(0; 0) đến đường thẳng Δ là
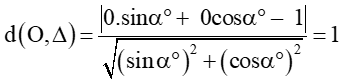
Do (sinαo)2 + (cosαo)2 = 1 với α là một số thực thuộc khoảng (0; 180).
b)
Giả sử (C) là đường tròn có tâm O và bán kính R = 1.
Với α là một số thực thuộc khoảng (0; 180) có thể thay đổi thì có:
d(O, Δ) = 1 = R không đổi
nên (C) luôn tiếp xúc với Δ.
Vậy phương trình đường tròn (C) cần tìm là x2 + y2 = 1.
Bài 7.27 trang 42 Sách bài tập Toán lớp 10 Tập 2: Vị trí của một chất điểm M tại thời điểm t (t trong khoảng thời gian từ 0 phút đến 180 phút) có toạ độ là (3 + 5sin t°; 4 + 5cos t°). Tìm toạ độ của chất điểm M khi M ở cách xa gốc toạ độ nhất.
Hướng dẫn giải:
Từ cách xác định toạ độ của chất điểm M ta có
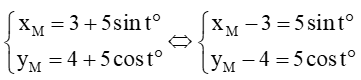
⇔ (xM – 3)2 + (yM – 4)2 = (5sin t°)2 + (5cos t°)2
⇔ (xM – 3)2 + (yM – 4)2 = 25(sin t°)2 + 25(cos t°)2
⇔ (xM – 3)2 + (yM – 4)2 = 25[(sin t°)2 + (cos t°)2]
⇔ (xM – 3)2 + (yM – 4)2 = 25.1
⇔ (xM – 3)2 + (yM – 4)2 = 25
Vậy chất điểm M luôn thuộc đường tròn (C) có tâm I(3; 4) và có bán kính R = = 5. Mặt khác gốc toạ độ O(0; 0) cũng thuộc đường tròn (C).
Do đó ta có: OM ≤ 2R = 10
Dấu bằng xảy ra khi và chỉ khi OM là đường kính của đường tròn (C), nghĩa là I là trung điểm của OM, điều đó tương đương với
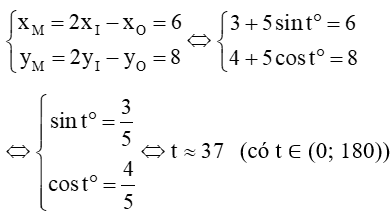
Vậy M(6; 8) thỏa mãn yêu cầu đề bài.
Lời giải sách bài tập Toán lớp 10 Bài 21: Đường tròn trong mặt phẳng tọa độ Kết nối tri thức hay khác:

