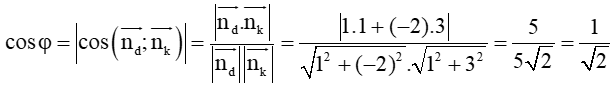Giải SBT Toán 10 trang 47 Tập 2 Kết nối tri thức
Với Giải SBT Toán 10 trang 47 Tập 2 trong Bài 22: Ba đường conic Sách bài tập Toán 10 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 10 trang 47.
Giải SBT Toán 10 trang 47 Tập 2 Kết nối tri thức
Bài 7.36 trang 47 Sách bài tập Toán lớp 10 Tập 2: Cho điểm M(x0; y0) thuộc elip (E) có phương trình .
a) Tính MF12 – MF22 theo x0; y0. Từ đó tính MF1, MF2, theo x0; y0.
b) Tìm điểm M sao cho MF2 = 2MF1.
c) Tìm M sao cho góc nhìn của M tới hai đểm F1; F2 (tức là góc ) là lớn nhất ?
Hướng dẫn giải:
Từ phương trình chính tắc của (E) ta có
b = 1, .
(E) có hai tiêu điểm là F1(–1; 0); F2(1; 0).
a)
Ta có:
MF12 = (x0 + 1)2 + (y0 – 0)2 = (x0 + 1)2 + y02
MF22 = (x0 – 1)2 + (y0 – 0)2 = (x0 – 1)2 + y02
MF12 – MF22
= (x0 + 1)2 + y02 – [(x0 – 1)2 + y02]
= (x0 + 1)2 – (x0 – 1)2
= x02 + 2x0 + 1 – (x02 – 2x0 + 1)
= 4x0.
Mặt khác, do M thuộc (E) nên ta có:
MF1 + MF2 = 2a = (1)
Mà: (MF1 – MF2)(MF1 + MF2) = MF12 – MF22
(2)
Cộng hai vế của (1) và (2) ta có:
2MF1 = +
⇔ MF1 = +
⇒ MF2 = .
b)
Sử dụng kết quả của phần a) ta có:
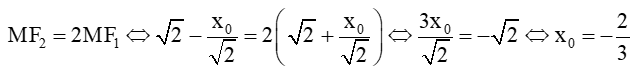
Mặt khác do M thuộc (E) nên ta có:
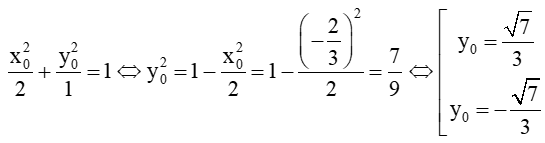
Vậy hoặc .
c)
Áp dụng định lí côsin trong tam giác MF1F2, ta có
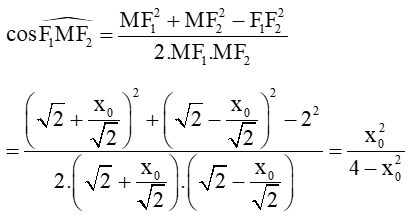
Ta có: ⇔ 0 ≤ x02 ≤ 2 ⇒ 4 – x02 > 0.
Suy ra
Dấu bằng xảy ra khi và chỉ khi x0 = 0 ⇒ y0 = ±1
Vậy M(0; 1) hoặc M(0; –1) thì M nhìn hai tiêu điểm dưới góc nhìn lớn nhất.
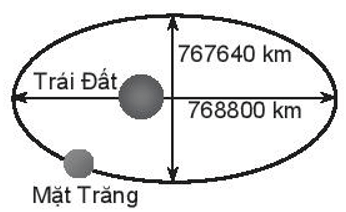
Bài 7.37 trang 47 Sách bài tập Toán lớp 10 Tập 2: Mặt Trăng chuyển động quanh Trái Đất theo quỹ đạo là một đường elip với tâm Trái Đất là một tiêu điểm. Độ dài trục lớn, độ dài trục nhỏ của quỹ đạo lần lượt là 768 800 km và 767 640 km. Tìm khoảng cách lớn nhất và bé nhất từ tâm của Trái Đất đến Mặt Trăng.
Hướng dẫn giải:
Xét đường elip như hình vẽ:

Theo đề bài: Độ dài trục lớn, độ dài trục nhỏ của quỹ đạo lần lượt là 768 800 km và 767 640 km. Nên ta có:
2a = 768 800 và 2b = 767 640
Do đó, a = 384 400 và b = 383 820.
Từ đó suy ra .
Vì vậy,
Khoảng cách lớn nhất từ tâm của Trái Đất đến Mặt Trăng là
a + c ≈ 384 400 + 21 108 = 405 508 (km)
Khoảng cách nhỏ nhất từ tâm của Trái Đất đến Mặt Trăng là:
a – c ≈ 384 400 – 21 108 = 363 292 (km).
Bài 7.38 trang 47 Sách bài tập Toán lớp 10 Tập 2: Trong các phương trình sau, phương trình nào là phương trình chính tắc của đường hypebol?
A. 16x2 – 5y2 = –80;
B. x2 = 4y;
C. ;
D. .
Hướng dẫn giải:
Đáp án đúng là: C
Phương trình chính tắc của đường hypebol có dạng . (trong đó a, b > 0)
Do đó, là một phương trình chính tắc của đường hypebol.
Bài 7.39 trang 47 Sách bài tập Toán lớp 10 Tập 2: Cho hai điểm A(–1; 0) và B(–2; 3). Phương trình đường thẳng đi qua B và vuông góc với AB là
A. x – 3y + 11 = 0;
B. x – 3y + 1 = 0;
C. –x – 3y + 7 = 0;
D. 3x + y + 3 = 0.
Hướng dẫn giải:
Đáp án đúng là: A
Đường thẳng đi qua B và vuông góc với AB nhận vectơ là vectơ pháp tuyến.
Phương trình đường thẳng đi qua B và vuông góc với AB là:
–1(x + 2) + 3(y – 3) = 0
⇔ –x + 3y – 2 – 9 = 0
⇔ x – 3y + 11 = 0.
Bài 7.40 trang 47 Sách bài tập Toán lớp 10 Tập 2: Cho điểm A(2; 3) và đường thẳng d: x + y + 3 = 0. Khoảng cách từ điểm A đến đường thẳng d là
A. ;
B. ;
C. 8;
D. .
Hướng dẫn giải:
Đáp án đúng là: B
Khoảng cách từ điểm A đến đường thẳng d là:
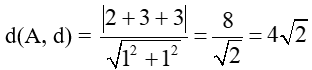
Bài 7.41 trang 47 Sách bài tập Toán lớp 10 Tập 2: Cho hai đường thẳng d: x – 2y – 5 = 0 và k: x + 3y + 3 = 0. Góc giữa hai đường thẳng d và k là
A. 30°;
B. 135°;
C. 45°;
D. 60°.
Hướng dẫn giải:
Đáp án đúng là: C
Xét d: x – 2y – 5 = 0 và k: x + 3y + 3 = 0 có các vectơ pháp tuyến lần lượt là:
Gọi φ là góc giữa hai đường thẳng d và k.
Ta có:
Vậy góc giữa hai đường thẳng là φ = 45°.
Lời giải sách bài tập Toán lớp 10 Bài 22: Ba đường conic Kết nối tri thức hay khác: