Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AB, BC
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AB, BC. Chứng minh rằng bốn điểm M, N, C, D không cùng nằm trong một mặt phẳng.
Giải SBT Toán 11 Cánh diều Bài 1: Đường thẳng và mặt phẳng trong không gian
Bài 4 trang 94 SBT Toán 11 Tập 1: Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AB, BC. Chứng minh rằng bốn điểm M, N, C, D không cùng nằm trong một mặt phẳng.
Lời giải:
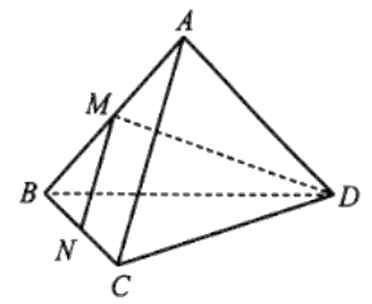
Giả sử bốn điểm M, N, C, D cùng thuộc một mặt phẳng.
Khi đó, M ∈ (NCD) nên M ∈ (BCD).
Như vậy, BM ⊂ (BCD), mà M ∈ AB nên A ∈ (BCD). Mâu thuẫn với giả thiết ABCD là tứ diện.
Vậy bốn điểm M, N, C, D không cùng nằm trong một mặt phẳng.
Lời giải Sách bài tập Toán lớp 11 Bài 1: Đường thẳng và mặt phẳng trong không gian hay khác:
Bài 1 trang 94 SBT Toán 11 Tập 1: Cho hình chóp tứ giác S.ABCD có ABCD là hình bình hành. Điểm M thuộc cạnh SC. Trong các mặt phẳng sau, điểm M nằm trên mặt phẳng nào? ....
Bài 2 trang 94 SBT Toán 11 Tập 1: Cho hình tứ diện ABCD. Giao tuyến của hai mặt phẳng (ABC) và (CDA) là đường thẳng ....
Bài 3 trang 94 SBT Toán 11 Tập 1: Một đồ vật trang trí có bốn mặt phân biệt là các tam giác (Hình 7). Vẽ hình biểu diễn của đồ vật đó ....
Bài 5 trang 95 SBT Toán 11 Tập 1: Cho hai mặt phẳng (P), (Q) cắt nhau theo giao tuyến d và hai đường thẳng a, b lần lượt nằm trong (P), (Q) ....
Bài 6 trang 95 SBT Toán 11 Tập 1: Cho tứ diện ABCD. Trên các cạnh AC, CD lần lượt lấy các điểm E, F sao cho CE = 3EA, DF = 2FC ....
Bài 7 trang 95 SBT Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M, N, P lần lượt là trung điểm của các cạnh SA, BC, CD ....
Bài 8 trang 95 SBT Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M, N, P lần lượt là trung điểm của các cạnh SA, SB, SC ....
Bài 9 trang 95 SBT Toán 11 Tập 1: Cho hình chóp tứ giác S.ABCD có đáy không là hình thang. Gọi O là giao điểm của AC và BD ....

