Bài 43 trang 45 SBT Toán 11 Tập 2

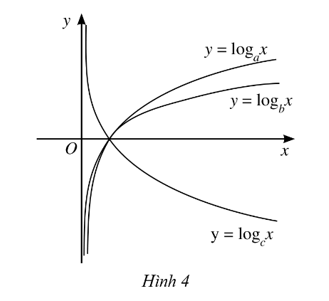
Cho ba số thực dương a, b, c khác 1 và đồ thị của ba hàm số lôgarit y = logx, y = logx, y = logx được cho bởi . Kết luận nào sau đây là đúng đối với ba số a, b, c?

Giải sách bài tập Toán 11 Bài 3: Hàm số mũ. Hàm số lôgarit

Bài 43 trang 45 SBT Toán 11 Tập 2: Cho ba số thực dương a, b, c khác 1 và đồ thị của ba hàm số lôgarit y = log_ax, y = log_bx, y = log_cx được cho bởi Hình 4. Kết luận nào sau đây là đúng đối với ba số a, b, c?

A. c > b > a;

B. a > b > c;

C. b > a > c;

D. c > a > b.

Lời giải:

Đáp án đúng là: C

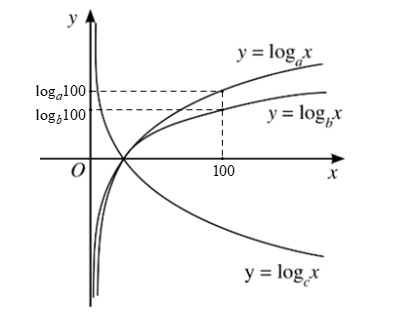
Hàm số lôgarit y = log_c x nghịch biến trên (0; +∞) nên 0 < c < 1. (1)

Hàm số lôgarit y = log_ax, y = log_bx đồng biến trên (0; +∞) nên a > 1 và b > 1 (2)

Với x = 100, từ đồ thị ta thấy:

${\log }_{a}100>{\log }_{b}100>0$

$\iff \frac{1}{{\log }_{100}a}>\frac{1}{{\log }_{100}b}$

$\iff \frac{1}{{\log }_{100}a}>\frac{1}{{\log }_{100}b}$

$\iff {\log }_{100}a<{\log }_{100}b\iff a<b$ (do 100 > 1) (3)

Từ (1), (2) và (3) ta có: b > a > c.

Lời giải SBT Toán 11 Bài 3: Hàm số mũ. Hàm số lôgarit hay khác:

• Bài 34 trang 44 SBT Toán 11 Tập 2: Tập xác định của hàm số y = 0,2^{x – 1} là:....

• Bài 35 trang 44 SBT Toán 11 Tập 2: Tập xác định của hàm số y = log₃(2x + 1) là:....

• Bài 36 trang 44 SBT Toán 11 Tập 2: Tập xác định của hàm số y = log₅(x²) là:....

• Bài 37 trang 44 SBT Toán 11 Tập 2: Trong các hàm số sau, hàm số có tập xác định ℝ là:....

• Bài 38 trang 44 SBT Toán 11 Tập 2: Trong các hàm số sau, hàm số nghịch biến trên tập xác định của nó là:....

• Bài 39 trang 44 SBT Toán 11 Tập 2: Trong các hàm số sau, hàm số đồng biến trên tập xác định của nó là:...

• Bài 40 trang 44 SBT Toán 11 Tập 2: Giá trị thực của tham số a để hàm số y = log_2a+3 x đồng biến trên khoảng (0; +∞) là:....

• Bài 41 trang 44 SBT Toán 11 Tập 2: Cho $a^{\frac{7}{3}}<a^{\frac{7}{8}}$${\log }_b\left(\sqrt{2}+\sqrt{5}\right)<{\log }_b\left(\sqrt{2}+\sqrt{3}\right).$ Kết luận nào sau đây đúng?....

• Bài 42 trang 45 SBT Toán 11 Tập 2: Đường nào sau đây là đồ thị hàm số y = 4^x? ....

• Bài 44 trang 45 SBT Toán 11 Tập 2: Lập bảng biến thiên và vẽ đồ thị hàm số:....

• Bài 45 trang 45 SBT Toán 11 Tập 2: Dựa vào đồ thị hàm số, cho biết với giá trị nào của x thì đồ thị hàm số y = (0,5)^x .....

• Bài 46 trang 45 SBT Toán 11 Tập 2: Dựa vào đồ thị hàm số, cho biết với giá trị nào của x thì đồ thị hàm số y = log₃x:....

• Bài 47 trang 46 SBT Toán 11 Tập 2: Tìm tập xác định của các hàm số:a) $y={\left(\frac{1}{2}\right)}^{2x-5};$....

• Bài 48 trang 46 SBT Toán 11 Tập 2: Tìm tất cả giá trị của tham số m để hàm số y = log₃(4x² – 4x + m) xác định trên ℝ.....

• Bài 49 trang 46 SBT Toán 11 Tập 2: Tìm tất cả giá trị của tham số a để hàm số $y={\log }_{a^2-2a+1}x$ nghịch biến trên khoảng (0; +∞).....

• Bài 50 trang 46 SBT Toán 11 Tập 2: Cho hàm số: $f\left(x\right)=\frac{9^x}{9^x+3}.$....

• Bài 51 trang 46 SBT Toán 11 Tập 2: Các nhà khoa học xác định được chu kì bán rã của ${}_6{}^{14}C$ là 5 730 năm, tức là sau 5 730 năm thì ....

• Bài 52 trang 46 SBT Toán 11 Tập 2: Mức cường độ âm L (dB) được tính bởi công thức $L=10\log \frac{I}{{10}^{-12}},$ trong đó I (W/m²) là cường độ âm....