Chứng minh rằng trong một hình hộp, tổng bình phương của bốn đường chéo bằng tổng bình phương

Chứng minh rằng trong một hình hộp, tổng bình phương của bốn đường chéo bằng tổng bình phương của tất cả các cạnh.

Giải SBT Toán 11 Cánh diều Bài 5: Hình lăng trụ và hình hộp

Bài 44 trang 113 SBT Toán 11 Tập 1: Chứng minh rằng trong một hình hộp, tổng bình phương của bốn đường chéo bằng tổng bình phương của tất cả các cạnh.

Lời giải:

Trước hết ta chứng minh một kết quả trong hình học phẳng: Trong hình bình hành, tổng bình phương của hai đường chéo bằng tổng bình phương tất cả các cạnh.

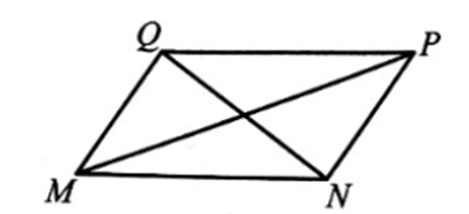
Xét hình bình hành MNPQ:

Chứng minh rằng trong một hình hộp, tổng bình phương của bốn đường chéo bằng tổng bình phương

Áp dụng định lí côsin trong các tam giác MPQ và QPN, ta có:

MP² = QM² + QP² – 2QM . QP . cos $\hat{M Q P}$

QN² = PQ² + PN² – 2PQ . PN . cos $\hat{Q P N}$

Do QM = PN và $\cos \hat{M Q P} = - \cos \hat{Q P N}$ (do hai góc bù nhau) nên ta có:

MP² + QN² = 2(QM² + QP²).

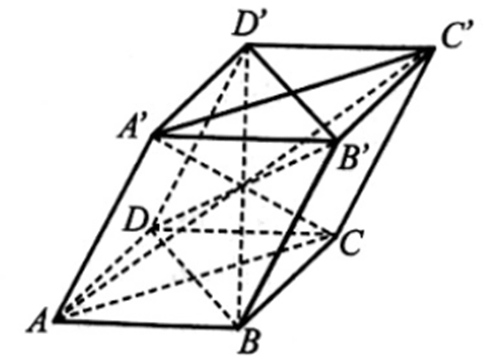
Xét hình hộp ABCD.A'B'C'D':

Chứng minh rằng trong một hình hộp, tổng bình phương của bốn đường chéo bằng tổng bình phương

Áp dụng kết quả trên cho hai hình bình hành AA'C'C và BB'D'D ta được:

AC'² + A'C² = 2(AA'² + A'C'²)

BD'² + B'D² = 2(BB'² + B'D'²)

Suy ra AC'² + A'C² + BD'² + B'D² = 4AA'² + 2(A'C'² + B'D'²) (do AA' = BB').

Mặt khác, trong hình bình hành A'B'C'D', ta có: A'C'² + B'D'² = 2(A'B'²+ A'D'²).

Vậy AC'² + A'C² + BD'² + B'D² = 4AA'² + 4A'B'² + 4A'D'².

Từ đó suy ra điều phải chứng minh.

Lời giải Sách bài tập Toán lớp 11 Bài 5: Hình lăng trụ và hình hộp hay khác:

Sách bài tập Toán 11

Chứng minh rằng trong một hình hộp, tổng bình phương của bốn đường chéo bằng tổng bình phương

Giải SBT Toán 11 Cánh diều Bài 5: Hình lăng trụ và hình hộp

Xem thêm lời giải Sách bài tập Toán 11 Cánh diều hay, chi tiết khác: