Cho hình chóp S.ABCD có đáy là hình thang ABCD, AD // BC, AD = 2BC
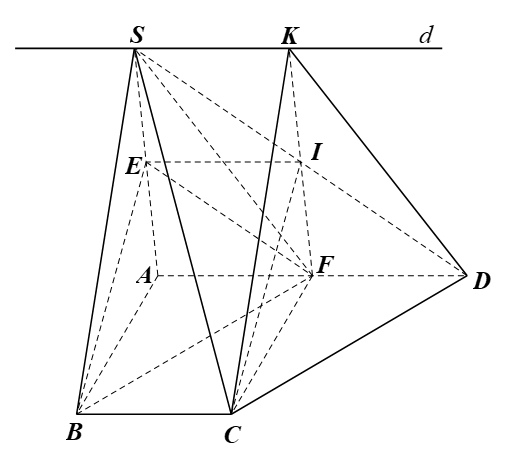
Cho hình chóp S.ABCD có đáy là hình thang ABCD, AD // BC, AD = 2BC. Gọi E, F, I lần lượt là trung điểm của các cạnh SA, AD, SD.
Giải sách bài tập Toán 11 Bài 4: Hai mặt phẳng song song - Chân trời sáng tạo
Bài 1 trang 127 SBT Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy là hình thang ABCD, AD // BC, AD = 2BC. Gọi E, F, I lần lượt là trung điểm của các cạnh SA, AD, SD.
a) Chứng minh: (BEF) // (SCD) và CI // (BEF).
b) Tìm giao tuyến của hai mặt phẳng (SBC) và (SAD).
c) Tìm giao điểm K của FI với giao tuyến vừa tìm được ở câu b, từ đó chứng minh (SBF) // (KCD).
Lời giải:
a) • Xét ∆SAD có E, F lần lượt là trung điểm của các cạnh SA, AD nên EF là đường trung bình của tam giác SAD, suy ra EF // SD.
Mà SD ⊂ (SCD), suy ra EF // (SCD).
Ta có F là trung điểm của AD nên AF = FD = AD,
Mà AD = 2BC hay BC = AD nên BC = AF = FD.
Lại có BC // AD hay BC // FD
Do đó tứ giác BFDC là hình bình hành nên BF // CD
Mà CD ⊂ (SCD)
Suy ra BF // (SCD).
Ta có: EF // (SCD);
BF // (SCD);
EF ∩ BF = F trong (BEF).
Suy ra (BEF) // (SCD).
• Xét ∆SAD có: E, I lần lượt là trung điểm của SA, SD
Suy ra EI là đường trung bình của ∆SAD, do đó EI // AD và EI = AD
Mà AD // BC và BC = AD
Suy ra EI // BC và EI = BC = AD
Do đó tứ giác EICB là hình bình hành nên CI // BE.
Mặt khác BE ⊂ (BEF), suy ra CI // (BEF).
b) Ta có BC // AD, BC ⊂ (SBC) và AD ⊂ (SAD)
Suy ra giao tuyến của (SBC) và (SAD) là đường thẳng d đi qua S và d // BC // AD.
c) Do d ⊂ (SAD) và FI ⊂ (SAD) nên trong mặt phẳng (SAD), ta có d ∩ FI = K.
Xét ∆SAD có I là trung điểm của SD, F là trung điểm của AD.
Suy ra IF là đường trung bình của ∆SAD, suy ra IF // SA hay KF // SA (1)
Mặt khác, SK // AF (2).
Từ (1) và (2) suy ra SKFA là hình bình hành, do đó SK = AF.
Suy ra SK = FD (vì AF = FD).
Tứ giác SKDF có SK = FD và SK // FD, nên SKDF là hình bình hành.
Suy ra SF // KD.
Ta có SF // KD và KD ⊂ (KCD) nên SF // (KCD).
BF // DC và DC ⊂ (KCD) nên BF // (KCD).
Lại có, trong (SBF) thì SF ∩ BF = F
Suy ra (SBF) // (KCD).
Lời giải Sách bài tập Toán lớp 11 Bài 4: Hai mặt phẳng song song hay khác: