Bảng 20 và Bảng 21 lần lượt biểu diễn mẫu số liệu ghép nhóm về nhiệt độ không khí

---

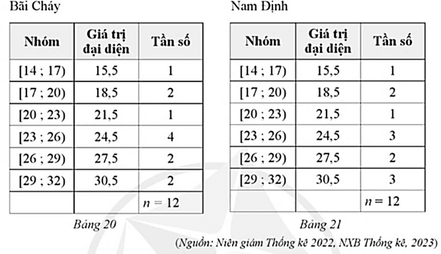
Bảng 20 và Bảng 21 lần lượt biểu diễn mẫu số liệu ghép nhóm về nhiệt độ không khí trung bình các tháng năm 2022 tại Bãi Cháy (Quảng Ninh) và Nam Định (đơn vị: độ C).

Giải SBT Toán 12 Cánh diều Bài tập cuối chương 3

Bài 16 trang 98 SBT Toán 12 Tập 1: Bảng 20 và Bảng 21 lần lượt biểu diễn mẫu số liệu ghép nhóm về nhiệt độ không khí trung bình các tháng năm 2022 tại Bãi Cháy (Quảng Ninh) và Nam Định (đơn vị: độ C).

a) Tính khoảng biến thiên, khoảng tứ phân vị, phương sai, độ lệch chuẩn của mẫu số liệu ghép nhóm của Bãi Cháy và Nam Định.

b) Trong hai địa điểm Bãi Cháy và Nam Định, địa điểm nào có nhiệt độ không khí trung bình tháng đồng đều hơn?

Lời giải:

a)

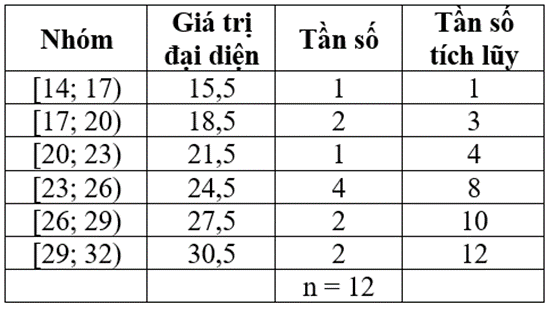
• Đối với mẫu số liệu ghép nhóm ở Bảng 20 của Bãi Cháy, ta có:

Khoảng biến thiên: R = 32 – 14 = 18.

Có $\frac{n}{4}=\frac{12}{4}=3$ nên nhóm 2 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 3.

Do đó, Q₁ = 17 + $\left(\frac{3-1}{2}\right).3$= 20.

Có $\frac{3n}{4}=\frac{3.12}{4}=9$nên nhóm 5 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 9.

Do đó, Q₃ = 26 + $\left(\frac{9-8}{2}\right).3$ = 27,5.

Suy ra khoảng tứ phân vị: ∆Q = Q₃ – Q₁ = 27,5 – 20 = 7,5.

Số trung bình cộng: ${\overline{x}}_1$= $\frac{1.15,5+2.18,5+1.21,5+4.24,5+2.27,5+2.30,5}{12}$ = 24.

Phương sai:

$s_1^2$= $\frac{1}{12}$[1 . (15,5 – 24)² + 2 . (18,5 – 24)² + 1 . (21,5 – 24)² + 4 . (24,5 – 24)²

 + 2 . (27,5 – 24)² + 2 . (30,5 – 24)²] = 20,75.

Độ lệch chuẩn: s₁ = $\sqrt{20,75}$≈ 4,5552.

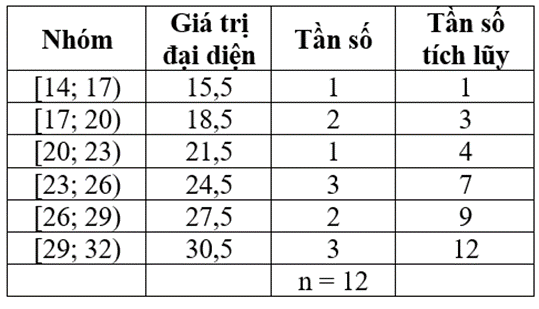
• Đối với mẫu số liệu ghép nhóm ở Bảng 21 của Nam Định, ta có:

Khoảng biến thiên: R' = 32 – 14 = 18.

Có $\frac{n}{4}=\frac{12}{4}=3$nên nhóm 2 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 3.

Do đó, Q'₁ = 17 + $\left(\frac{3-1}{2}\right).3$= 20.

Có $\frac{3n}{4}=\frac{3.12}{4}=9$nên nhóm 5 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 9. Do đó, Q'₃ = 26 + $\left(\frac{9-7}{2}\right).3$= 29.

Suy ra khoảng tứ phân vị: ∆Q' = Q'₃ – Q'₁ = 29 – 20 = 9.

Số trung bình cộng: ${\overline{x}}_2$= $\frac{1.15,5+2.18,5+1.21,5+3.24,5+2.27,5+3.30,5}{12}$= 24,5.

Phương sai:

$s_2^2$= $\frac{1}{12}$[1 . (15,5 – 24,5)² + 2 . (18,5 – 24,5)² + 1 . (21,5 – 24,5)² + 3 . (24,5 – 24,5)²

 + 2 . (27,5 – 24,5)² + 3 . (30,5 – 24,5)²] = 24.

Độ lệch chuẩn: s₂ = $\sqrt{24}$≈ 4,899.

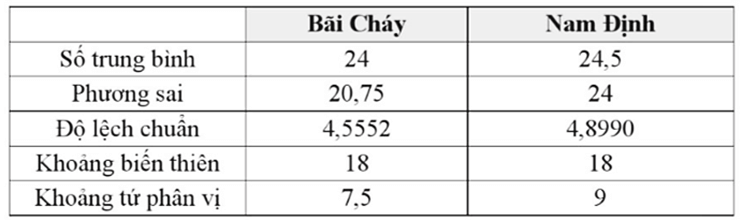
Vậy ta có bảng sau:

b) Do s₁ < s₂ (4,5552 < 4,899) nên nhiệt độ ở Bãi Cháy đồng đều hơn.

Lời giải SBT Toán 12 Bài tập cuối chương 3 hay khác:

• Bài 13 trang 97 SBT Toán 12 Tập 1: Khi thống kê chiều cao (đơn vị: centimét) của 120 nữ sinh khối 12 ....

• Bài 14 trang 97 SBT Toán 12 Tập 1: Một mẫu số liệu ghép nhóm có tứ phân vị thứ nhất, thứ hai, thứ ba ....

• Bài 15 trang 97 SBT Toán 12 Tập 1: Cho mẫu số liệu ghép nhóm như Bảng 19 ....

• Bài 17 trang 98 SBT Toán 12 Tập 1: Bảng 22 thống kê độ ẩm không khí trung bình các tháng năm 2022 ....