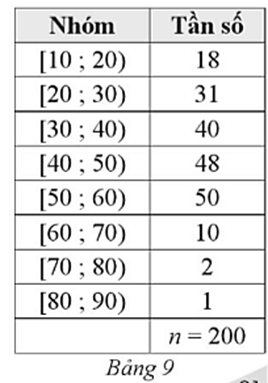
Khi điều tra độ tuổi của dân cư trong một khu phố (đơn vị: tuổi) được kết quả cho bởi Bảng 9

Khi điều tra độ tuổi của dân cư trong một khu phố (đơn vị: tuổi) được kết quả cho bởi Bảng 9.

Giải SBT Toán 12 Cánh diều Bài 1: Khoảng biến thiên, khoảng tứ phân vị của mẫu số liệu ghép nhóm

Bài 6 trang 91 SBT Toán 12 Tập 1: Khi điều tra độ tuổi của dân cư trong một khu phố (đơn vị: tuổi) được kết quả cho bởi Bảng 9.

a) Khoảng biến thiên của mẫu số liệu ghép nhóm đó là: R = 90 (tuổi).
b) Nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng $\frac{n}{4} = \frac{200}{4} = 50$ .
c) Q₃ = $52 \frac{17}{24}$ .
d) Khoảng tứ phân vị của mẫu số liệu lớn hơn 20.

Lời giải:

a) S

b) Đ

c) S

d) Đ

Trong mẫu số liệu ghép nhóm trên, ta có: đầu mút trái của nhóm 1 là a₁ = 10, đầu mút phải của nhóm 8 là a₉ = 90.

Vậy khoảng biến thiên của mẫu số liệu ghép nhóm đó là:

R = a₉ – a₁ = 90 – 10 = 80 (tuổi).

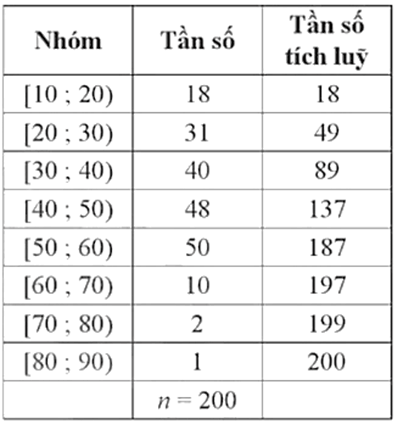
Ta có bảng sau:

Khi điều tra độ tuổi của dân cư trong một khu phố (đơn vị: tuổi) được kết quả cho bởi Bảng 9

Ta có: $\frac{n}{4} = \frac{200}{4} = 50$ .

Nhận thấy 49 < 50 < 89 nên nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 50.

Xét nhóm 3 là nhóm [30; 40) có s = 30, h = 10, n₃ = 40 và nhóm 2 là nhóm [20; 30) có cf₂ = 49.

Ta có: Q₁ = s + $(\frac{50 - c f_{2}}{n_{3}}) . h$ = 30 + $(\frac{50 - 49}{40}) .10$ = 30,25 (tuổi).

Có $\frac{3 n}{4} = \frac{3.200}{4} = 150$ .

Nhận thấy 137 < 150 < 187 nên nhóm 5 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 150.

Xét nhóm 5 là nhóm [50; 60) có đầu mút trái t = 50, độ dài l = 10, tần số n₅ = 50 và nhóm 4 là nhóm [40; 50) có tần số tích lũy cf₄ = 137.

Ta có: Q₃ = t + $(\frac{150 - c f_{4}}{n_{5}}) . l$ = 50 + $(\frac{150 - 137}{50}) .10$ = 52,6 (tuổi).

Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm đã cho là:

∆Q = Q₃ – Q₁ = 52,6 – 30,25 = 22,35 (tuổi).

Lời giải SBT Toán 12 Bài 1: Khoảng biến thiên, khoảng tứ phân vị của mẫu số liệu ghép nhóm hay khác: