SBT Toán 7 trang 45 Tập 1 Cánh diều

---

Haylamdo biên soạn và sưu tầm lời giải SBT Toán 7 trang 45 Tập 1 trong Bài 3: Giá trị tuyệt đối của một số thực. Với lời giải chi tiết nhất hy vọng sẽ giúp học sinh dễ dàng nắm được cách làm bài tập SBT Toán lớp 7.

Giải SBT Toán 7 trang 45 Tập 1 Cánh diều

Bài 19 trang 45 sách bài tập Toán lớp 7 Tập 1: Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai? Vì sao?

a) Giá trị tuyệt đối của một số thực là một số dương hoặc bằng 0.

b) Hai số có giá trị tuyệt đối bằng nhau là hai số bằng nhau.

c) Giá trị tuyệt đối của một số thực luôn bằng chính nó.

Lời giải:

a) Đúng. Do giá trị tuyệt đối của một số thực là một số không âm.

b) Sai. Do hai số có giá trị tuyệt đối bằng nhau là hai số bằng nhau hoặc đối nhau.

c) Đúng. Do hai số đối nhau có điểm biểu diễn cách đều điểm gốc 0 nên giá trị tuyệt đối của chúng bằng nhau.

d) Sai. Do giá trị tuyệt đối của số âm là số đối của nó.

Bài 20 trang 45 sách bài tập Toán lớp 7 Tập 1: Tìm:

|−2 022|; $\left(\sqrt{312}\right)$ ; $\left(-\sqrt{\mathrm{5,4}}\right)$ ; $\left(\frac{-273}{2}\right)$ ; |−20,21|.

Lời giải:

Ta có: |−2 022| = −(−2 022) = 2 022; $\left(\sqrt{312}\right)=\sqrt{312}$ ;

$\left(-\sqrt{\mathrm{5,4}}\right)=-\left(-\sqrt{\mathrm{5,4}}\right)=\sqrt{\mathrm{5,4}}$; $\left(\frac{-273}{2}\right)=-\left(\frac{-273}{2}\right)=\frac{273}{2}$ ;

|−20,21| = −(−20,21) = 20,21.

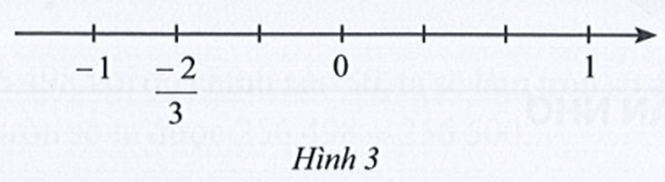
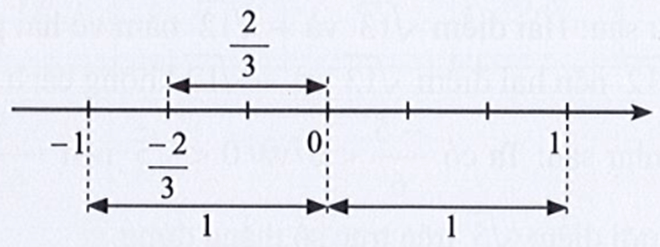
Bài 21 trang 45 sách bài tập Toán lớp 7 Tập 1: Biểu diễn trên trục số giá trị tuyệt đối của mỗi số đã cho trên trục số ở Hình 3:

Lời giải:

Trên trục số ở Hình 3 có các điểm −1; $\frac{-2}{3}$ ; 0; 1.

Giá trị tuyệt đối của các số −1; $\frac{-2}{3}$ ; 0; 1 lần lượt là 1; $\frac{2}{3}$ ; 0; −1.

Ta biểu diễn giá trị tuyệt đối của các số −1; $\frac{-2}{3}$ ; 0; 1 trên trục số như sau:

Bài 22 trang 45 sách bài tập Toán lớp 7 Tập 1: Tính giá trị của mỗi biểu thức:

a) |−11| + |22| + |−33| − 44;

b) 2 . |−21| − 3 . |125| − 5 . |−33| − |2 . 21|;

c) $\mathrm{2,8}+3.\left(-\frac{13}{3}\right)+\mathrm{0,2}.\left|6\right|+5.|-10|$ ;

d) $(-\mathrm{1,5})+2.\left(2\frac{1}{2}\right)-6.\left(\frac{-16}{3}\right)+5.|-\mathrm{0,3}|$ .

Lời giải:

a) |−11| + |22| + |−33| − 44

= 11 + 22 + 33 – 44

= 33 + 33 – 44

= 66 – 44 = 22.

b) 2 . |−21| − 3 . |125| − 5 . |−33| − |2 . 21|

= 2 . 21 − 3 . 125 − 5 . 33 – 42

= 42 – 375 – 165 – 42

= – 333 – 165 – 42

= – 498 – 42 = – 540.

c) $\mathrm{2,8}+3.\left(-\frac{13}{3}\right)+\mathrm{0,2}.\left|6\right|+5.|-10|$

$=\mathrm{2,8}+3.\frac{13}{3}+\mathrm{0,2}.6+5.10$

= 2,8 + 13 + 1,2 + 50

= 15,8 + 1,2 + 50

= 17 + 50 = 67.

d) $(-\mathrm{1,5})+2.\left(2\frac{1}{2}\right)-6.\left(\frac{-16}{3}\right)+5.|-\mathrm{0,3}|$ .

$=(-\mathrm{1,5})+2.\frac{5}{2}-6.\frac{16}{3}+5.\mathrm{0,3}$

= −1,5 + 5 – 32 + 1,5

= (−1,5 + 1,5) + (5 – 32)

= 0 – 27 = – 27.

Bài 23 trang 45 sách bài tập Toán lớp 7 Tập 1: Trong giờ hoạt động của câu lạc bộ Toán, bạn Nam phát biểu "Giá trị tuyệt đối của tổng hai số thực khác dấu bất kì luôn là một số dương". Bạn Nam phát biểu đúng hay sai? Vì sao?

Lời giải:

Phát biểu của bạn Nam là sai do giá trị tuyệt đối của tổng hai số đối là 0.

Chẳng hạn: |2 + (−2)| = |0| = 0.

Bài 24 trang 45 sách bài tập Toán lớp 7 Tập 1: Chọn dấu "<", ">", "=" thích hợp cho :

a) |-12| |0| ;

b) $\left(\frac{-321}{491}\right)$ $\left(\frac{321}{491}\right)$ ;

c) |5,706| |-7,01|;

d) $|-\sqrt{131}|$ 131 .

Lời giải:

a) Ta có: |−12| = 12 > 0 = |0|.

Do đó |-12| |0| ;

b) Ta có $\left(\frac{-321}{491}\right)=\frac{321}{491};\left(\frac{321}{491}\right)=\frac{321}{491}$ .

Do đó $\left(\frac{-321}{491}\right)$ $\left(\frac{321}{491}\right)$ ;

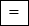
c) Ta có: |5,706| = 5,706; |−7,01| = 7,01.

Vì 5,706 < 7,01 nên |5,706| < |−7,01|.

Vậy |5,706| |-7,01|;

d) Ta có: $|-\sqrt{131}|=\sqrt{131}=\mathrm{11,4455...}$

Vì 11,4455 < 131 nên $\sqrt{131}<131$ .

Vậy $|-\sqrt{131}|$ 131 .

Bài 25 trang 45 sách bài tập Toán lớp 7 Tập 1: Tìm số thực x, biế

a) $\left|x\right|=\frac{13}{17}$ ;

b) |x + 2,037| = 0;

c) $|x-22|=-\sqrt{3}$ ;

d) |x| = x;

e*) |x| + |x + 1| = 0.

Lời giải:

a) Do $\left|x\right|=\frac{13}{17}$

Nên $x=\frac{13}{17}$ hoặc $x=-\frac{13}{17}$ .

b) Do |x + 2,037| = 0 nên x + 2,037 = 0.

Suy ra x = − 2,037.

c) Vì |x – 22| ≥ 0 với mọi số thực x.

Mà $-\sqrt{3}<0$ nên không có giá trị nào của x thỏa mãn $|x-22|=-\sqrt{3}$ .

d) Ta có |x| = x với mọi số thực x không âm.

Vậy x ≥ 0.

e*) Do |x| ≥ 0, |x + 1| ≥ 0 với mọi số thực x.

Nên |x| + |x + 1| ≥ 0 với mọi số thực x.

Do đó |x| + |x + 1| = 0 khi |x| = 0 và |x + 1| = 0.

Suy ra x đồng thời bằng 0 và bằng –1 (vô lí).

Vậy không có giá trị nào của x thỏa mãn yêu cầu của đề bài.

Lời giải Sách bài tập Toán lớp 7 Bài 3: Giá trị tuyệt đối của một số thực Cánh diều hay khác:

• Giải SBT Toán 7 trang 46 Tập 1