Giải SBT Toán 7 trang 57 Tập 2 Chân trời sáng tạo
Haylamdo biên soạn và sưu tầm lời giải SBT Toán 7 trang 57 Tập 2 trong Bài 6: Tính chất ba đường trung trực của tam giác Sách bài tập Toán lớp 7 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 7 trang 57.
Giải SBT Toán 7 trang 57 Tập 2 Chân trời sáng tạo
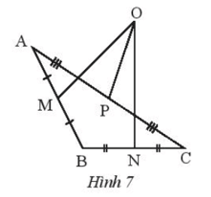
Bài 1 trang 57 sách bài tập Toán lớp 7 Tập 2: Điểm O trong Hình 7 có phải là giao điểm của ba đường trung trực của tam giác ABC hay không? Hãy giải thích.
Lời giải:
Vì OM không vuông góc với AB nên OM không phải đường trung trực của cạnh AB.
Suy ra O không phải là giao điểm của ba đường trung trực của tam giác ABC.
Vậy điểm O không phải là giao điểm của ba đường trung trực của tam giác ABC.
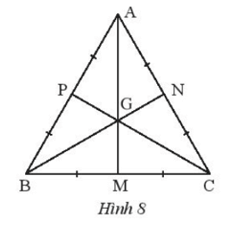
Bài 2 trang 57 sách bài tập Toán lớp 7 Tập 2: Cho tam giác đều ABC và điểm G như trong Hình 8. Hãy chứng minh GA = GB = GC.
Lời giải:
Vì tam giác ABC đều (giả thiết) nên AB = AC = BC.
Ta có: AB = AC, MB = MC.
Suy ra AM là trung trực của cạnh BC.
Ta có: BA = BC, NA = NC.
Suy ra BN là trung trực của cạnh AC.
Ta có: CA = CB, PA = PB.
Suy ra CP là trung trực của cạnh AB.
Xét ∆ABC có AM, BN, CP lần lượt là trung trực của cạnh BC, AC, AB.
Mà G là giao điểm của AM, BN, CP.
Suy ra GA = GB = GC (tính chất ba đường trung trực của tam giác).
Vậy GA = GB = GC.
Lời giải Sách bài tập Toán 7 Chân trời sáng tạo Bài 6: Tính chất ba đường trung trực của tam giác Chân trời sáng tạo hay khác: