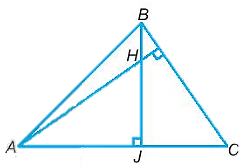
Gọi H là trực tâm của tam giác nhọn ABC. Khi AH = BC

Giải SBT Toán 7 Kết nối tri thức Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác

Bài 9.21 trang 58 sách bài tập Toán lớp 7 Tập 2: Gọi H là trực tâm của tam giác nhọn ABC. Khi AH = BC, hãy chứng minh $\hat{B A C} = 45 °$ .

Lời giải:

Gọi BJ là đường cao xuất phát từ B của tam giác ABC.

Xét hai tam giác AHJ và tam giác BCJ có:

AH = BC (gt)

$\hat{A J H} = \hat{B J C} (= 90 °)$

$\hat{J A H} = \hat{J B C}$ (hai góc cùng phụ với $\hat{J C B}$ )

Do đó ∆AHJ = ∆BCJ (cạnh huyền – góc nhọn).

Suy ra AJ = BJ (hai cạnh tương ứng).

Xét tam giác JAB vuông tại J có AJ = BJ (cmt) nên JAB là tam giác vuông cân tại J.

Vậy $\hat{B A J} = \hat{B A C} = 45 °$ (đpcm).